💷 🔵 👩🏿‍🤝‍👨🏾 支持向量机从头开始解释并在python中实现。支持向量法的详细分析 👋🏼 ⚖️ 🚼

各位选择ML武士之路的人大家好！

简介：

在本文中，我们考虑将支持向量机方法（例如Eng。SVM，支持向量机 ）用于分类问题。将介绍该算法的主要思想，分析设置权重的输出以及简单的DIY实现。以数据集为例 $虹膜$ 将演示在空间中具有线性可分离/不可分离数据的书面算法的操作 $R ^ 2$ 以及培训/预后的可视化。此外，还将宣布算法的优缺点，以及其修改方法。

图1.鸢尾花的开源照片

要解决的问题：

我们将解决二进制（只有两个类）分类的问题。首先，该算法在训练集中的对象上进行训练，对于这些对象而言，其类别标签是预先已知的。此外，已经训练好的算法会根据递延/测试样本为每个对象预测类别标签。类标签可以取值 $Y = \ {-1，+1 \}$ 。对象-带有N个标志的矢量 $x =（x_1，x_2，...，x_n）$ 在太空 $R ^ n$ 。学习时，算法应建立一个函数 $F（x）= y$ 这需要一个论点 $x$ -来自太空的物体 $R ^ n$ 并给出班级标签 $y$ 。

关于该算法的一般词汇：

分类任务涉及与老师一起教学。 SVM是一种具有老师的学习算法。在视觉上，可以在此顶级文章中找到许多机器学习算法（请参阅“机器学习世界地图”部分）。应该补充的是，SVM也可以用于回归问题，但是本文将对SVM分类器进行分析。

SVM作为分类器的主要目标是找到分离超平面的方程
$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$ 在太空 $R ^ n$ ，它将以某种最佳方式划分两个类别。转型的总体看法 $F$ 设施 $x$ 分类标签 $Y$ ： $F（x）=符号（w ^ Tx-b）$ 。我们会记得我们已经指定 $w =（w_1，w_2，...，w_n），b = -w_0$ 。设置算法权重后 $w$ 和 $b$ （训练），所有落在构造的超平面一侧的物体都将被预测为第一类，而另一侧的物体将被预测为第二类。

内部功能 $符号（）$ 对象属性与算法权重存在线性组合，这就是为什么SVM引用线性算法的原因。可以用不同的方法来构造分割超平面，但要使用SVM权重 $w$ 和 $b$ 配置这些对象，使类对象与分离的超平面距离尽可能远。换句话说，该算法使超平面与最接近它的类对象之间的间隙（ 英语边界 ）最大化。这样的对象称为支持向量（见图2）。因此，算法的名称。

图2. SVM（此处的基础图）

SVM比例调整规则的详细输出：

为了使分割的超平面距离采样点尽可能远，条带宽度应最大。向量 $w$ 是分割超平面的方向向量。在下文中，我们将两个向量的标量表示为 $\弯角a，b \弯角$ 或 $a ^ Tb$ 让我们找到向量的投影，其末端将是超平面方向向量上不同类别的支持向量。该投影将显示分隔带的宽度（见图3）：

图3.设置比例尺的规则的输出（来自此处的图的基础）

（ ） ， （ ， ， ） （ （ ） （ ） ）

$\ langle（x _ +-x _-），w / \ Arrowvert w \ Arrowvert \ rangle =（\ langle x _ +，w \ rangle-\ langle x _-，w \ rangle）/ \ Arrowvert w \ Arrowvert =（（b +1）-（b-1））/ \ Arrowvert w \ Arrowvert = 2 / \ Arrowvert w \ Arrowvert$

最 大

$2 / \ Arrowvert w \ Arrowvert \ rightarrow最大$

分 钟

$\ Arrowvert w \ Arrowvert \ rightarrow分钟$

（ ）

$（w ^ Tw）/ 2 \ rightarrow min$

对象x与类边界的边距是值 $M = y（w ^ Tx-b）$ 。当且仅当缩进时，算法才会在对象上产生错误 $M$ 否定（当 $y$ 和 $（w ^ Tx-b）$ 不同的字符）。如果 $M∈（0，1）$ ，则对象落在分隔带内。如果 $M> 1$ ，则对象x被正确分类，并且位于距分隔条一定距离的位置。我们记下此连接：

（ ）

$y（w ^ Tx-b）\ geqslant 1$

当不允许任何对象进入分隔带时，生成的系统是带有 硬边距SVM的默认SVM设置。它是通过Kuhn-Tucker定理解析地求解的。产生的问题等同于找到拉格朗日函数的鞍点的双重问题。

$$ display $$ \ left \ {\ begin {array} {ll}（w ^ Tw）/ 2 \ rightarrow min＆\ textrm {} \\ y（w ^ Tx-b）\ geqslant 1＆\ textrm {} \ end {array} \对。 $$显示$$

只要我们的课程是线性可分离的，那么所有这些都是好的。为了使该算法能够处理线性不可分割的数据，让我们对系统进行一些改动。让算法在训练对象上犯错误，但同时尽量减少错误。我们介绍了一组附加变量 $\ xi _i> 0$ 表征每个物体的误差大小 $x_i$ 。我们在最小化功能中引入了对总错误的惩罚：

$$ display $$ \ left \ {\ begin {array} {ll}（w ^ Tw）/ 2 + \ alpha \ sum \ xi _i \ rightarrow min＆\ textrm {} \\ y（w ^ Tx_i-b） \ geqslant 1-\ xi _i＆\ textrm {} \\ \ xi _i \ geqslant0＆\ textrm {} \ end {array} \对。 $$显示$$

我们将考虑算法错误的数量（当M <0时）。称其为惩罚。那么对所有对象的罚款将等于对每个对象的罚款额 $x_i$ 在哪里 $[M_i <0]$ -阈值功能（见图4）：

罚 金 总 和

$罚金= \总和[M_i <0]$

$$ display $$ [M_i <0] = \左\ {\开始{array} {ll} 1＆\ textrm {if} M_i <0 \\ 0＆\ textrm {if} M_i \ geqslant 0 \ end {array} \对。 $$显示$$

接下来，我们使惩罚对误差的大小敏感，同时引入了使对象接近类边界的惩罚：

$罚金= \ sum [M_i <0] \ leqslant \ sum（1- M_i）_ + = \ sum max（0,1-M_i）$

在惩罚表达式中添加术语 $\ alpha（w ^ Tw）/ 2$ 我们获得了一个对象的经典SVM损失函数，该函数具有软间隙 （ soft-margin SVM ）：

$Q =最大值（0,1- M_i）+ \ alpha（w ^ Tw）/ 2$

$Q =最大值（0,1- yw ^ Tx）+ \ alpha（w ^ Tw）/ 2$

$Q$ -损失函数，它也是损失函数。那就是我们将在手的实施过程中借助梯度下降来最小化的东西。我们得出改变权重的规则，其中 $\ eta$ -下降步骤：

$w = w-\ eta \ bigtriangledown Q$

$$ display $$ \ bigtriangledown Q = \左\ {\开始{array} {ll} \ alpha w-yx＆\ textrm {if} yw ^ Tx <1 \\ \ alpha w＆\ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \对。 $$显示$$

面试中可能出现的问题（基于真实事件）：

关于SVM的一般问题之后： 为什么Hinge_loss会最大化间隙？ -首先，请记住，当权重变化时，超平面会改变其位置 $w$ 和 $b$ 。当损失函数的梯度不等于零时（通常称其为“梯度流”），算法的权重开始改变。因此，我们特别选择了这样一种损失函数，其中梯度在适当的时间开始流动。 $铰链损失$ 看起来像这样： $H =最大值（0,1-y（w ^ Tx））$ 。记住间隙 $m = y（w ^ Tx）$ 。当差距 $m$ 足够大（ $1$ 或更多）表达 $（1-m）$ 变得小于零并且 $H = 0$ （因此，梯度不会流动，算法的权重也不会发生任何变化）。如果间隙m足够小（例如，当对象落入分隔带和/或为负（如果分类预测不正确），则Hinge_loss变为正（ $H> 0$ ），梯度开始流动，算法权重发生变化。总结：梯度在两种情况下流动：当样本对象落在分离带内时，以及对象分类不正确时。

要检查外语水平，可能会出现类似的问题： LogisticRegression与SVM之间的异同是什么？ -首先，我们将讨论相似性：这两种算法都是监督学习中的线性分类算法。损失函数的论点有些相似之处： $log（1 + exp（-y（w ^ Tx）））$ 对于logreg和 $最大值（0,1-y（w ^ Tx））$ 用于SVM（请参见图片4）。我们可以使用梯度下降来配置这两种算法。接下来让我们来谈谈差异：SVM返回对象的类标签，与LogReg不同，后者返回类成员的概率。 SVM无法与类标签一起使用 $\ {0,1 \}$ （不重命名类），与LogReg（LogReg的损失函数为 $\ {0,1 \}$ ： $-ylog（p）-（1-y）log（1-p）$ ，在哪里 $y$ -真实阶级的标签， $p$ -算法的回报，归属对象的概率 $x$ 上课 $\ {1 \}$ ）不仅如此，我们还可以解决不需梯度下降的Smar-margin问题。搜索支持向量的任务在拉格朗日函数中被简化为搜索鞍点-该任务仅指二次编程。

损失函数的代码：

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14});

图4.损失函数

经典软边际SVM的简单实现：

注意！您将在文章末尾找到完整代码的链接。以下是脱离上下文的代码块。有些块只能在计算出先前的块之后才能启动。在许多块下，将放置图片，以显示放置在其上方的代码的工作方式。

首先，我们将修剪所需的库和画线功能：

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l

软边距SVM的Python实现代码：

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w)

我们详细考虑每行代码的操作：

1）创建一个函数add_bias_feature（a） ，该函数自动扩展对象向量，并在每个向量的末尾添加数字1，以便“忘记”自由项b。表达方式 $w ^ Tx-b$ 等同于表达式 $w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$ 。我们有条件地假设单位是所有向量x的向量的最后一个分量，并且 $w_0 = -b$ 。现在设置权重 $w$ 和 $w_0$ 我们将在同一时间生产。

特征向量扩展功能代码：

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended

2）然后我们将描述分类器本身。它具有初始化init（） ，学习fit（） ，预测precise（） ，找到铰链_loss（）函数的损失以及找到带有软间隙soft_margin_loss（）的经典算法的函数的总损失的功能。

3）初始化后，引入了3个超参数：_etha-梯度下降步骤（ $\ eta$ ），_alpha-比例权重降低的速度系数（在损失函数中的二次项之前） $\ alpha$ ），_ epochs-训练时代的数量。

初始化功能代码：

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None

4）在训练每个训练样本时代（X_train，Y_train）的过程中，我们将从样本中选取一个元素，计算该元素与给定时间的超平面位置之间的距离。此外，根据此间隙的大小，我们将使用损失函数的梯度来更改算法的权重 $Q$ 。同时，我们将为每个时期计算该函数的值以及每个时期改变权重的次数。在开始培训之前，我们将确保没有超过两个不同的班级标签真正进入学习功能。在设置余额之前，请使用正态分布对其进行初始化。

学习功能代码：

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch)

检查书面算法的操作：

检查我们的书面算法是否适用于某种玩具数据集。取虹膜数据集。我们将准备数据。将第1类和第2类表示为 $+ 1$ ，并将0类设为 $-1$ 。使用PCA算法（在此处进行说明和应用），我们以最小的数据丢失将4个属性的空间最佳地减少为2个（对于我们来说，观察训练和结果将更加容易）。接下来，我们将分为训练（训练）样本和延迟（验证）样本。我们将在训练样本上进行训练，预测并检查是否延期。我们选择学习因素，以使损失函数下降。在训练期间，我们将研究训练和延迟采样的损失函数。

数据准备块：

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)

初始化和培训单位：

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show()

所得分隔条的可视化块：

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show()

预测可视化块：

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show()

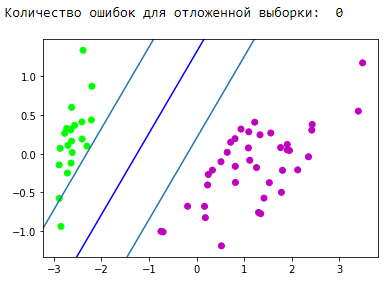
太好了！我们的算法处理线性可分离的数据。现在，将类别0和1与类别2分开：

数据准备块：

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)

初始化和培训单位：

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show()

所得分隔条的可视化块：

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show()

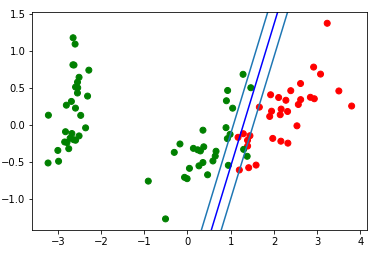
让我们看一下gif，它将显示分割线在训练过程中的位置变化（仅500帧用于更改权重。连续的前300帧。接下来的每130帧200幅）：

动画创建代码：

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick')

预测可视化块：

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show()

拉直空间

重要的是要理解，在实际问题中，线性可分离的数据不会是简单的情况。为了处理此类数据，提出了移动到另一个空间的想法，在该空间中数据将是线性可分离的。这样的空间称为整流。精简空间和内核不会在本文中受到影响。您可以在E. Sokolov的14,15,16简介和K.V. Vorontsov的讲座中找到最完整的数学理论。

从sklearn使用SVM：

实际上，几乎所有经典的机器学习算法都是为您编写的。让我们给出一个代码示例，我们将从sklearn库中获取算法。

代码示例

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None))

经典SVM的优缺点：

优点：

在较大的特征空间下工作良好；
处理少量数据时效果很好；
因此，该算法找到了最大的划分带，就像安全气囊一样，可以减少分类错误的数量；
由于该算法简化为解决凸域中的二次规划问题，因此，该问题始终具有唯一的解决方案（始终只有一个具有某些算法超参数的分离超平面）。

缺点：

培训时间长（适用于大型数据集）；
噪声不稳定：训练数据中的异常值成为入侵者的参考对象，并直接影响分离超平面的构造；
没有描述在类的线性不可分的情况下最适合特定问题的构造内核和纠正空间的通用方法。选择有用的数据转换是一门艺术。

SVM应用程序：

一种或另一种机器学习算法的选择直接取决于在数据挖掘过程中获得的信息。但总的来说，可以区分以下任务：

具有少量数据的任务；
文本分类任务。 SVM提供了良好的基线（[预处理] + [TF-iDF] + [SVM]），因此预测的准确度在某些卷积/递归神经网络的水平上（我建议您尝试使用此方法来巩固材料）。这里给出了一个很好的例子，“第3部分。我们教的其中一个技巧的例子” 。
对于具有结构化数据的许多任务，链接[功能工程] + [SVM] + [内核]“静态蛋糕”；
由于铰链损耗被认为非常快，因此可以在Vowpal Wabbit中找到它（默认情况下）。

算法修改：

支持向量方法有多种添加和修改，旨在消除某些缺点：

相关向量机（RVM）
1标准SVM（LASSO SVM）
双正则化SVM（ElasticNet SVM）
支持功能机器（SFM）
相关特征机（RFM）

SVM的其他来源：

沃龙佐夫（K.V. Vorontsov）的文字讲座
E.Sokolov的摘要-16.15.16
Alexandre Kowalczyk的酷消息
在habr上有2篇关于svm的文章：
- 2010年
- 2018年
在github上，我可以在以下链接中突出显示2个很棒的SVM实现：
- 来自国内开发商的ML算法
- 从零开始的ML

结论：

非常感谢您的关注！如有任何意见，反馈和提示，我将不胜感激。
您将在github上找到本文的完整代码。

ps感谢yorko提供了平滑角的技巧。感谢物理和技术部门Aleksey Sizykh，他对代码进行了部分投资。

支持向量机 从头开始解释并在python中实现。 支持向量法的详细分析

More articles:

支持向量机从头开始解释并在python中实现。支持向量法的详细分析