下午好
正如我在第一篇文章中所承诺的那样,我想让您熟悉一种解决Diophantine方程组的方法。 本文的目的是使其他读者熟悉这种技术,并以或多或少可以理解的方式进行传播。
考虑两个Diophantine方程组
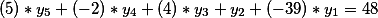
和

我们找到了第一个方程式的所有可能解。 你怎么问? 当然有不同的方法,但是我将在以下文章之一中分享如何解决类似的问题。 现在,我们假设一般解决方案具有以下形式

如何检查我没有说谎?
只需调用矩阵演算并将我们的第一个Diophantine方程(没有自由项)的值的矢量乘以所有系数的矩阵就足够了。

结果获得了自由项的值,因此计算是正确的
下一步是替代我们的通用解决方案。

进入第二个方程

步骤是相同的:我们将第二个方程的系数中的向量乘以第一个方程的一般解
我们得到这个结果
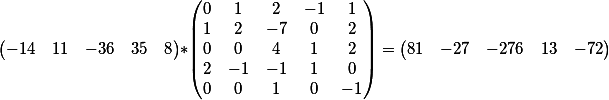
也就是说,我们得到了以下形式的等式
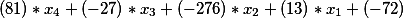
在第二个Diophantine方程的右侧,因为有一个等于-335的自由项,所以它仍然存在,也就是说,我们在此阶段的最终解的形式为
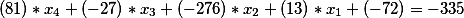
或将免费会员移到右边,我们得到
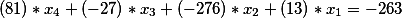
因此,我们得到了下一个Diophantine方程。 让我们找到它的一般解决方案,并测试其正确性。

也就是说,一般的解决方案是
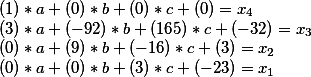
现在,我们正在进行逆变换(称为逆变换)。 即系统

我们用最后一个阶段的结果代替未知的x
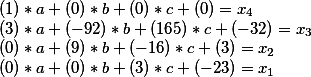
在矩阵演算中,这可以通过将一个矩阵乘以另一个矩阵来解决。
但是对于第一个矩阵,您需要执行特定的过程:(暂时)删除具有自由成员的最后一列,因为此参数不参与乘法运算,将在以后使用。
两个矩阵相乘的结果生成
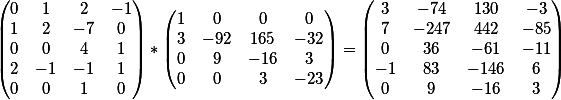
矩阵
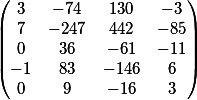
最后一列是该系统的免费成员。
我们考虑了乘法之前暂时删除的列,并添加了它们
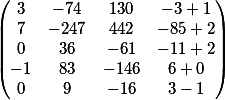
我们以矩阵形式给出的最终答案
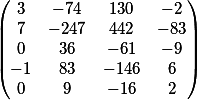
看看吗?
第一个方程的系数与矩阵的向量积
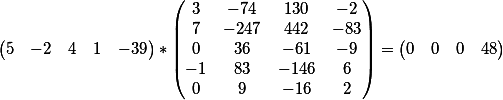
第二个方程的系数与矩阵的向量积
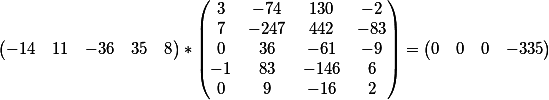
如您所见,结果与每个方程的自由项一致。
因此,一般解决方案的形式为
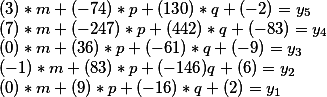
其中m,p,q-可以采用任何整数值
以这种直接的方式,有可能解决更复杂的线性双色子方程。 在此算法之后创建了一个真正的计算器 ;该计算器确实不喜欢出现零而不是出现在初始系统的第一个方程的系数中的值。 但这是我对此算法的具体实现的问题。
在下一个主题中,我将告诉您如何使用常规解决方案的矩阵来创建双色子方程。 这项任务通常是平庸的,只能一次完成,但是突然有人不知道。
谢谢您的意见,反馈和建议。