几个世纪以来，研究人员一直在寻找有关理想流体的流体动力学欧拉方程不正确的情况的例子。 最后，数学家找到了这样的例子。
在某些简化的情况下，当液环彼此接近时，描述其运动的欧拉方程不起作用多年来，数学家一直怀疑在某些条件下
，欧拉方程将无法工作。 但是，他们无法描述发生这种情况的具体情况。 直到今天
这些方程是流体运动的理想数学描述。 在某些假设下，他们模拟了池塘中波浪的传播或罐中糖蜜的渗透。 他们应该能够描述在任何条件下任何液体的运动，而且已经过去了两个多世纪。
但是，新证据表明，在某些条件下，这些方程式仍然无效。
加利福尼亚大学圣地亚哥分校的数学家
塔雷克·埃尔金迪 （
Tarek Elgindi）说：“一年半以前，我什至说我一生都没有看到这样的发展。”
Elgindi与
Tejeddin Gole和
Nader Masmudi合作，在2019年出版的两本著作中证明了欧拉方程中存在缺陷-他本人写了《
April》和《
October》 。 这项工作对这些著名的液体方程式进行了一个世纪的假设。
普林斯顿大学的数学家
彼得·康斯坦丁说：“我认为这是一个了不起的成就。”
埃尔金迪的著作并未带来欧拉方程式的终结。 它证明了在完全确定的条件下，方程似乎过热并开始胡扯。 但是在更现实的条件下，到目前为止，这些方程式仍然是无懈可击的。
但是，埃尔金迪发现的异常使数学家感到惊讶，因为它发生在如先前认为的方程仍应正常工作的条件下。
纽约大学数学家
弗拉德·维科尔 （
Vlad Vikol）说：“总的来说，我觉得人们对塔雷克（Tarek）的榜样感到惊讶。
欧拉方程组是如何奔波的
伦纳德·欧拉（Leonhard Euler）导出了液体方程式，该方程式在1757年以他的名字命名。 它们描述了流体随时间的变化，就像牛顿方程描述了台球在桌子上的运动一样。
更精确地，这些方程式表示液体的微小颗粒的瞬时运动。 他们的描述包括粒子的速度（粒子移动的速度和方向）以及与
涡旋相关的量（粒子以顶部的方式旋转以及以哪个方向旋转）。
所有这些信息完全形成一个“速度场”，即在给定时间点的流体运动的快照。 欧拉方程以初始速度场开始，并预测其在将来的任何时间将如何变化。
塔雷克·埃尔金迪（Tarek Elgindi）欧拉方程式并不从字面上描述现实世界的流体。 这些包括一些非物理假设。 例如，它们仅在流体中的内部流动不产生彼此相对运动的摩擦时起作用。 还假定了液体的不可压缩性，也就是说，根据欧拉方程的规则，不可能将液体放置在比其已经占用的体积小的空间中来压缩液体。
明尼苏达大学的
弗拉基米尔·斯维拉克 （
Vladimir Sverak）通过电子邮件向我们写道：“可以将这种模型想象为理想化的世界，将方程式视为该世界运动的规则。”
这些不寻常的条件使数学家和物理学家约翰·冯·诺伊曼开玩笑地说这些方程式模拟了“干水”的行为。 为了模拟经受内部摩擦（所谓的粘度）的更逼真的流体，研究人员使用
了Navier-Stokes方程 。
欧拉方程非常理想。 康斯坦丁说，在真正的液体中存在摩擦。
但与此同时，欧拉方程在科学领域仍占有重要地位。 研究人员想知道这些方程式是否在没有摩擦和压缩的理想化世界框架内清晰地工作，也就是说，它们是否可以描述速度场所有可能初始版本的所有未来状态。 或者，换句话说：是否存在这些方程无法建模的流体运动？
“从本质上讲，问题很简单：这些方程式总是能发挥作用吗？” Sverak说。
从理论上讲，将液体当前状态的值代入方程式，您将获得精确的数量来描述其未来状态。 然后，您可以再次将这些新值代入方程式，并扩展您的预测。 通常，以后可以在任何时间长度内继续进行类似的过程。
但是，在极少数情况下方程也可能会破裂。 它们会吱吱作响，喘气，产生适合将来输入参数作用的输出值，然后突然产生根本不适合它们的值。 在这种情况下，数学家说方程是“匆忙的”。
如果欧拉方程组出现问题，那是因为它们开始以某种不自然的方式增加了该点的速度或涡度。 该增益将如此强大，以至于在有限的时间内，点的速度或涡旋变得无穷大。 一旦方程式给出一个无穷大的值，它们就会分解并不再描述未来的任何环境条件。 这是因为通常不可能用无穷大的值进行计算-这等于除以零（顺便说一下，这种情况下的速度值将超过光速-尽管在模型的理想化世界中这并不是最坏的情况）。
这些命运的无限含义被称为“奇异性”。 当数学家问：“欧拉方程总是起作用吗？”时，他们实际上在问：“在某些情况下欧拉方程会给出奇异性？”
许多数学家认为-到目前为止，他们还没有找到方程式真正爆发的特定情形。
康斯坦丁说：“有一种感觉，欧拉试图避免这种怪异，直到最近，他才成功。”
这项新工作并未证明在数学家最感兴趣的条件下方程如何给出奇异性。 但是，到目前为止，这个结果比其他结果更接近目标。 为此，Elgindi考虑了流体运动的简化模型。
降低复杂度
数学家有许多减少流体运动复杂性的方法，他们使用欧拉方程进行模拟。 许多最有趣的结果与Elgindi取得的结果相似，包括一个演示，您可以简化流体的行为多少-也就是可以简化替换方程式的数据的数量-同时仍然可以对方程本身说一些有意义的事情。
在真实的三维流体（例如池塘中的水）中，任何粒子都具有三个可能的运动轴：x轴（左右），y轴（上下）和z轴（前后）。 大量的行动自由。 此外，颗粒在液体的一部分中的运动将不一定与颗粒在另一部分中的运动紧密相关。
“您必须跟踪太多，”埃尔金迪说。
在新论文中，Elgindi简化了Euler方程的工作。 它要求液体沿z轴对称，这在实际液体中通常是找不到的。 由于对称性，因为已知z轴两侧的点都是镜像对称的，所以计算速度场变得更加容易。 因此，如果您知道一个点的速度或涡度，则只需更改这些值的符号，并获得另一点的这些值。
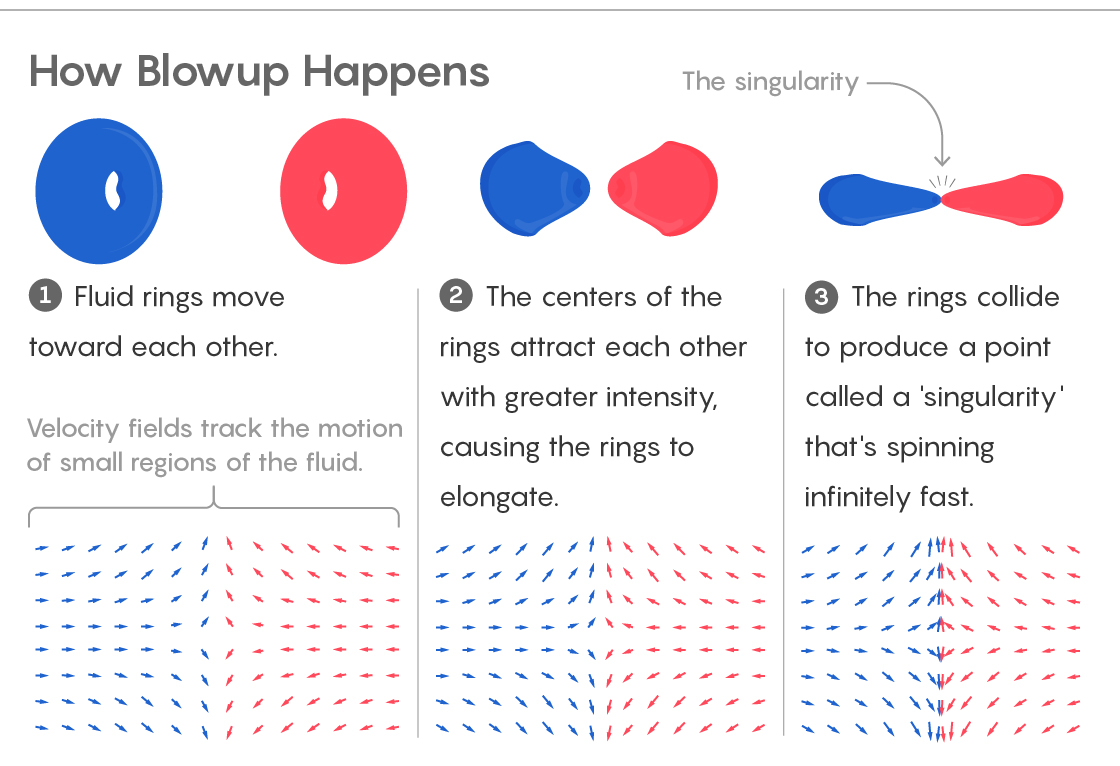1）流体流向。 速度场跟踪小部分流体的运动。
2）环的中心被吸引，导致环拉伸。
3）环碰撞，形成“奇点”，并以无限的速度旋转。它还限制了流体中点的可能运动。 粒子可以沿z轴移动，也可以远离z轴移动，也可以朝z轴移动。 它们不能绕z轴旋转。 数学家说，这种液体中没有漩涡。
“这将任务减少到二维，”埃尔金迪说。
最后，Elgindi对引入欧拉方程的初始数据施加了更多条件。 从某种意义上讲，这些数据要比描述真实流体的数据更粗糙，并增加了形成奇异点的可能性。
在现实生活中，如果您从一个点移动到非常靠近它的另一点，那么这两点的速度将几乎相等。 这两个点的涡旋也应该非常相似。 数学家说，具有此属性的速度场是“平滑的”，也就是说，当从一个点移动到另一个点时，速度场上的值逐渐或平滑地变化。 没有快速的变化。
但是在描述Elgindi液体的情况下，一切都不同。
Vikol说：“ Tarek数据的变化可能会发生很大变化。” “近点可能具有非常不同的涡旋。”
Elgindi的简化似乎与实际液体的行为大相径庭，以便发挥作用。 但是，它们仍然比许多科学家以前考虑过欧拉方程的简化方案的刚性要低得多。 实际上，埃尔金迪甚至表明，在这些简化的条件下（但不是太多），欧拉方程开始产生非常出乎意料的结果。
游戏结束
要了解Elgindi的发现，请想象一个盛有水的容器。 这不是一个确切的例子，因为Elgindi的工作考虑的是无边界的液体，即在零重力下像气泡一样飞行。 但是，为了使脚本可视化（这是他工作的核心），将水倒入水箱中会很有用。 尽管最重要的数学假设以及最难以证明的数学假设都涉及无边界的液体。
然后想象一下位于水箱不同末端的两个厚水环。 它们形成小的漏斗，例如漩涡-流体内部的有组织的扰动。 在自然界中发现了类似的现象，类似于有经验的吸烟者会散发出的烟圈。
现在想象一下两个相对的环如何组合在一起。
在进近过程中，欧拉方程正常运行，计算描述每个时刻流体的速度场。 但是，当它们彼此靠得很近时，这些方程式开始产生非常奇怪的结果。
它们显示了环如何开始越来越相互吸引-环的中心点甚至比外部更相互吸引。 结果，环被延伸，并开始类似于漏斗。 圆环的中心越靠近，它们的速度增加得越快。 然后它们发生碰撞。
现在，如果您查看描述碰撞的速度场，您会发现在整个Euler方程历史中，通过这组假设，没有人看到：奇点。 Elgindi证明了Euler方程在碰撞点给出无限的速度。 游戏结束了。
“方程式的经典形式被打破了，”埃尔金迪说。 “在那之后，目前还不清楚发生了什么。”
结果有其局限性。 即，不可能根据此结果在完全“平滑”的条件下外推欧拉方程的行为。 几十年前的数学家证明，在“平稳”条件下，埃尔金迪所考虑的情况不会产生奇异性。
但是，他的其余结果完全改变了数学家对这些旧方程式的看法。
在埃尔金迪工作之前，数学家无法证明无边界流体中的任何情况的存在，在这种情况下，欧拉方程组工作了一段时间（当环在一起时），但是不是无限的。 在以前的所有著作中，数学家都证明，如果方程基本上起作用，那么它们总是起作用。
“这是一个非常了不起的结果，因为它证明了场景中存在奇异点，我们称之为'正确定义'。” 这是有道理的，但与此同时，我们在有限的时间内达到了唯一性，”康斯坦丁说。
许多代科学家一直在寻找欧拉方程的弱点。 最后-有所保留-数学家找到了他。