格雷码与
希尔伯特曲线有着密切的联系。
但是，当与同事交流时，发现这种简单的沉迷在他们眼中看来是不平凡的。 在Wiki上，Internet搜索只是给出了一个模糊的短语：“更大维空间中的希尔伯特曲线代表格雷码的概括”。 因此，希望以简单的语言简短地打开该主题。
结果，削减了“丑闻，阴谋，调查”。
格雷码的主要特征是两个在字典上相邻的值仅在一个类别中不同。 另一方面，希尔伯特曲线是连续的-两个相邻点之间的距离始终是一个。 仅此就暗示了它们的内在联系。
格雷码描述了单个超立方体内希尔伯特曲线的出现。 实际上，如果我们采用3位代码并将其绘制在3维空间中（将每一位用作对应的坐标），我们得到
图1 3位格雷码作为3维立方体熟悉的图片是希尔伯特曲线的3维单形！ 用相同的单纯形连续替换单纯形的每个节点（考虑到旋转和反射以保持连续性），我们获得了希尔伯特曲线4x4x4。
继续进行这些迭代，我们可以连续填充任意大小的立方晶格。
图2希尔伯特曲线的单纯形的几次迭代。但是怎么发生的呢？
众所周知，格雷码是自相似的。 由于更改顺序时值的前一半等于后一半（高位除外），因此有时称为“镜像”。 最重要的一点就是反转。” 为了清楚起见，3位代码是最高有效位-最左侧：
因为我们在谈论自相似，所以让我们从头开始-用一位代码。 严格来说，可以从零维开始-点，这从根本上不会改变任何东西，只是必须多写一些单词。
格雷的一位数字编码甚至比三线步枪还要简单，它是0或1。
在几何上，这对应于一维单位立方体-一个段。 您可以从头到尾，也可以从头到尾沿着线段移动-直至对称，这是相同的。 但是，尽管如此，我们将开始的地方称为值较小的地方（请记住，多维数据集的边是数字的数字），而结束的地方则称为较大的地方。
我们转向二维情况。 二维立方体是正方形。 考虑到自相似性，我们克隆一维立方体（0,1）并得到两个线段-（0,0-> 1,0）和（0,1-> 1,1）。 现在，您需要连接这些线段以绕过广场。 这里出现两个选择：
- 我们将上一个迭代的开始-一维立方体与其克隆的开始连接起来。 直到对称为止，这与将末端连接到末端相同。 对称的类型是镜像。 此选项有条件地称为“传教士”。
- 我们将上一个迭代的结尾与其克隆的开头联系起来。 直到对称为止，这与将行的开头与克隆的结尾连接在一起相同。 对称类型是中心。 我们将此选项称为“火车”。
在传递三个或更多维的情况时，我们的行为类似。
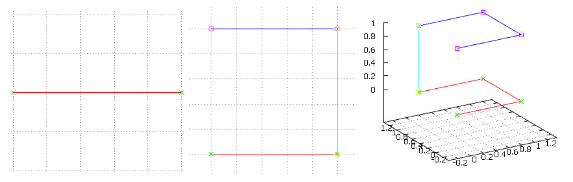图3“传教士”版本的前两次迭代在此，上一个迭代以红色突出显示，其克隆以蓝色突出显示，并且它们的连接为青绿色。
请注意，连接始终通过一个维度-新添加的维度，因此格雷码的主要特征是由于自相似而出现的。 并且由于上一迭代的末尾与克隆的末尾有关，因此发生了“镜像”-当四处走动时，我们被迫以相反的顺序进行克隆。 不论尺寸。 在这里，您可以看到希尔伯特曲线的原点和特征-不管（任何尺寸）晶格有多大，在基层，它都是一个长度为1的单位立方体。
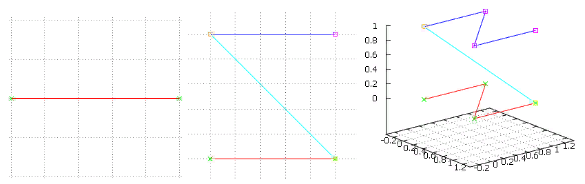图4选项“ train”的前两次迭代，颜色相同但是这种音乐我们也很熟悉-我们得到了单曲
Z曲线 。 这里的“单纯形”一词还意味着，如果我们取其每个点并用单纯形替换，我们将得到一个4x4x4的立方体，并进行连续迭代-我们可以填充任意大的立方晶格。
有趣的是，在这种情况下，从原点传递到代码的路径（可以解析为位）的转换是微不足道的。
格雷码的情况是G = W ^（W >> 1），其中W是传递的长度，G是格雷码。
图5 Z曲线的前两次迭代（Wiki）
6个比较，希尔伯特曲线的前两个迭代（wiki）但是，没有其他（自然）的选择可以规避单个超立方体。
事实证明，无论您在
希尔伯特（Hilbert），勒贝格（Lebesgue）和空虚的任何地方投掷。
PS ：在标题图片中，是带有八位格雷码的圆形编码器。
PPS ：在这里，他们更正了我，认为
单纯形是一个公认的术语，不好用。 好吧，本文不仅是单纯形，而且是希尔伯特曲线的单纯形或Z曲线的单纯形。 愿忠实的数学家原谅我。