视觉信息论（第2部分）

Longrid的翻译的第二部分专门研究信息理论中的概念可视化。 第二部分处理熵，交叉熵，Kullback-Leibler发散，互信息和分数位。 所有概念都提供了出色的视觉解释。

为了完整理解，在阅读第二部分之前，建议您熟悉第一部分 。

熵计算

回想一下一条消息的花费很长 $$$L$ 等于 $$$\ frac {1} {2 ^ L}$ 。 我们可以将该值取反，以得到值得给定数量的消息长度： $$$\ log_2（\ frac {1} {cost}）$ 。 既然我们花了 $$$p（x）$ 每个代码字 $$$x$ ，长度将相等 $$$\ log_2（\ frac {1} {p（x）}）$ 。 在图中，选择了最佳码字长度。



前面我们讨论过，从给定的概率分布中传达事件的平均消息长度有一个基本限制 $$$p$ 。 使用最佳编码系统时，此限制即平均消息长度称为熵 $$$p，H（p）$ 。 现在我们知道了最佳码字长度，我们可以计算出来了！

$$

$$H（p）= \ sum_xp（x）\ log_2 \ Bigg（\ frac {1} {p（x）} \ Bigg）$$

（通常，熵写为 $$$H（p）=-\和p（x）\ log_2（p（x））$ 使用平等 $$$\日志（1 / a）=-\日志（a）$ 。 在我看来，第一个版本更加直观，因此我们将继续使用它。）

如果我想报告发生了什么事件，那么无论我做什么，平均而言，我需要发送这么多位。

传输某物所需的平均信息量直接影响压缩。 但是，还有其他原因值得我们注意吗？ 是的 它描述了我的不确定性，并使量化信息成为可能。

如果我确定会发生什么，就完全不必发送消息！ 如果有两件事以50％的概率发生，我只需要发送1位。 但是，如果有64个不同的事件以相同的概率发生，那么我将不得不发送6位。 概率越集中，我就越有机会用短消息创建智能代码。 可能性越模糊，我的帖子就应该越长。

结果越不确定，当他们告诉我发生了什么时，我平均就会学到更多。

交叉熵

鲍勃在移居澳大利亚之前不久，也嫁给了同样有想象力的爱丽丝。 令我惊讶的是，以及让我脑海中其他角色感到惊讶的是，爱丽丝不是爱狗人士。 她是个爱猫的人。 尽管如此，他们还是能够在对动物的普遍迷恋和非常有限的词汇中找到共同的语言。



这两个词使用相同的词，只是频率不同。 鲍勃一直在谈论狗，爱丽丝一直在谈论猫。

爱丽丝首先使用鲍勃的代码向我发送了消息。 不幸的是，她的职位超过了要求。 Bob的代码已针对其概率分布进行了优化。 爱丽丝的概率分布不同，代码对她而言并不是最佳的。 Bob使用其代码时的平均码字长度为1.75位；当Alice使用其代码时，则为2.25位。 如果两者不那么相似，那就更糟了！

来自一种分布的平均消息长度（具有另一种分布的最佳代码）称为交叉熵。 形式上，我们可以定义交叉熵，如下所示：

$$

$$H_p（q）= \ sum_xq（x）\ log_2 \ Bigg（\ frac {1} {p（x）} \ Bigg）$$

在这种情况下，我们谈论的是爱丽丝（Alice）的cat虫的词频相对于鲍勃（Bob）的爱犬者的词频的交叉熵。



为了减少我们的连接成本，我请爱丽丝使用她自己的代码。 令我欣慰的是，这减少了其平均邮件长度。 但是，这带来了一个新问题：有时候，鲍勃不小心使用了爱丽丝的代码。 令人惊讶的是，鲍勃使用爱丽丝的代码比爱丽丝使用鲍勃的代码更糟！

因此，现在我们有四种可能性：

• 鲍勃使用本机代码（ $$$H（p）= 1.75$ 位）
• 爱丽丝使用鲍勃的代码（ $$$H_p（q）= 2.25$ 位）
• 爱丽丝使用自己的代码（ $$$H（q）= 1.75$ 位）
• 鲍勃使用爱丽丝的代码（ $$$H_q（p）= 2.375$ 位）

这并不像人们想象的那样直观。 例如，我们可以看到 $$$H_p（q）≠H_q（p）$ 。 我们能以某种方式看到这四个含义是如何相互联系的吗？

在下图中，每个子图表示这4种可能性之一。 插图显示了一条消息的平均长度。 它们以正方形组织，因此，如果消息来自相同的分布，则图表位于附近，并且如果它们使用相同的代码，则它们彼此重叠。 这使您可以直观地将发行版和代码组合在一起。



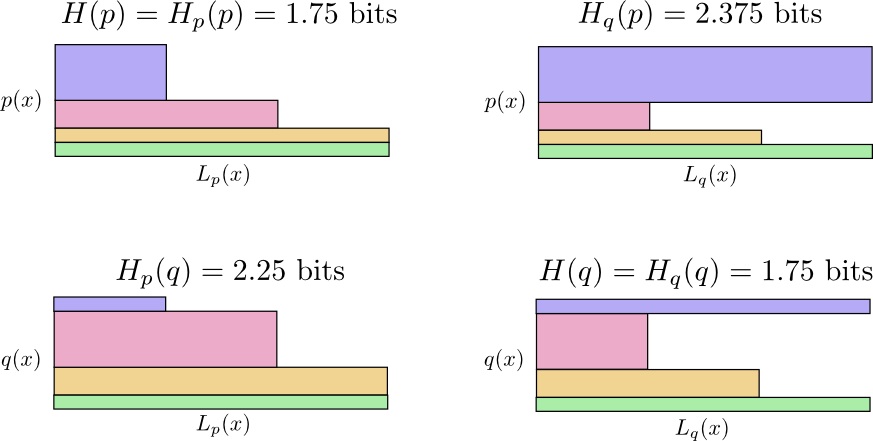
看看为什么 $$$H_p（q）≠H_q（p）$ ？ $$$H_q（p）$ 这么大，因为标为蓝色的事件通常发生在 $$$p$ 但会得到一个很长的代码字，因为它对于 $$$q$ 。 另一方面，频繁发生的事件 $$$q$ 少见 $$$p$ 但差异不大，因此 $$$H_p（q）Hp（q）$ 少一点。

交叉熵不是对称的。

那么，为什么要关心交叉熵呢？ 交叉熵为我们提供了一种表达两种概率分布的差异的方法。 分布越不同 $$$p$ 和 $$$q$ 更大的交叉熵 $$$p$ 关于 $$$q$ 会有更多的熵 $$$p$ 。



同样，更多 $$$q$ 与...不同 $$$p$ 更大的交叉熵 $$$q$ 关于 $$$p$ 会有更多的熵 $$$q$ 。

真正有趣的是熵和交叉熵之间的区别。 这种差异等于我们的帖子有多长时间，因为我们使用的代码针对其他发行版进行了优化。 如果分布相同，则该差异将为零。 随着差异的增加，它将变得更大。

我们称这种差异为Kullback-Leibler散度，或简称为KL散度。 吉隆坡分歧 $$$p$ 关于 $$$q$ ， $$$D_q（p）$ 定义如下：

$$

$$D_q（p）= H_q（p）-H（p）$$

KL散度的最大优点是看起来像两个分布之间的距离。 它可以衡量它们有多不同！ （如果认真对待这个想法，那么您将进入信息几何。）

交叉熵和KL散度在机器学习中非常有用。 通常，我们希望一种分布与另一种分布接近。 例如，我们可能希望预测的分布接近基本事实。 KL差异为我们提供了一种自然的方式，因此它在任何地方都可以体现出来。

熵和几个变量

让我们回到前面给出的天气和衣服示例：




我的母亲和许多父母一样，有时会担心我的着装不适合天气。 （她很有怀疑的理由-冬天有时我不穿雨衣。）因此，她经常想知道天气和我穿的衣服。 我应该发给她多少位举报？

考虑这一点的最简单方法是使概率分布均匀：



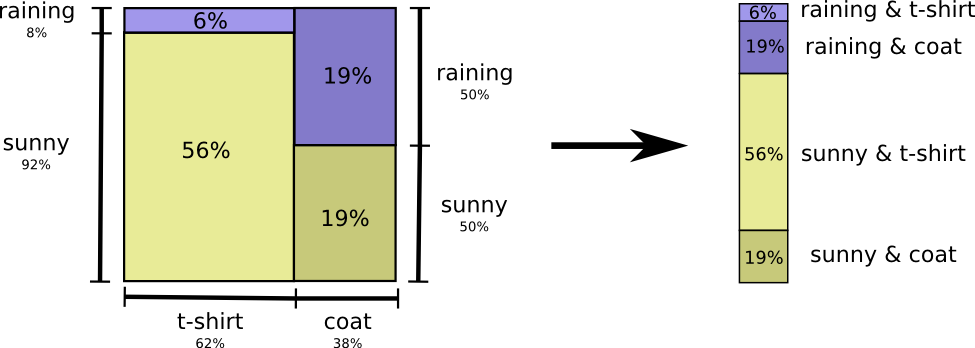
现在，我们可以为具有此类概率的事件计算最佳代码字，并计算平均消息长度：



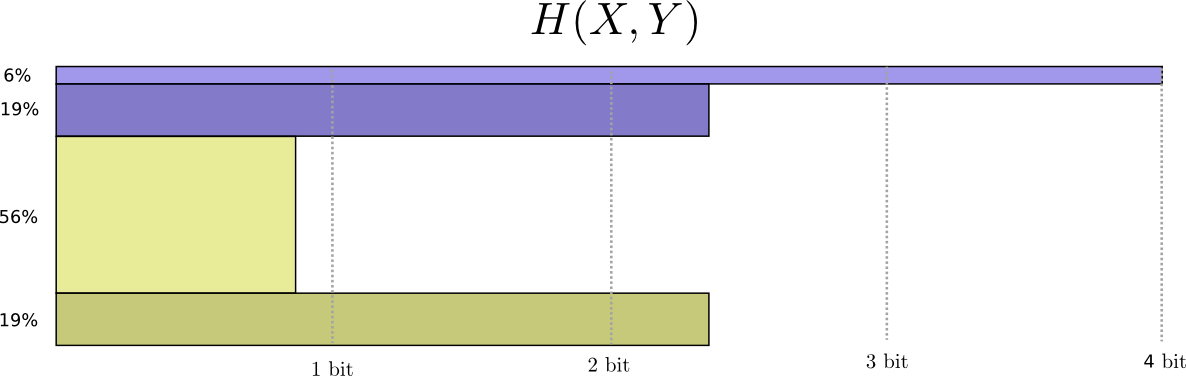
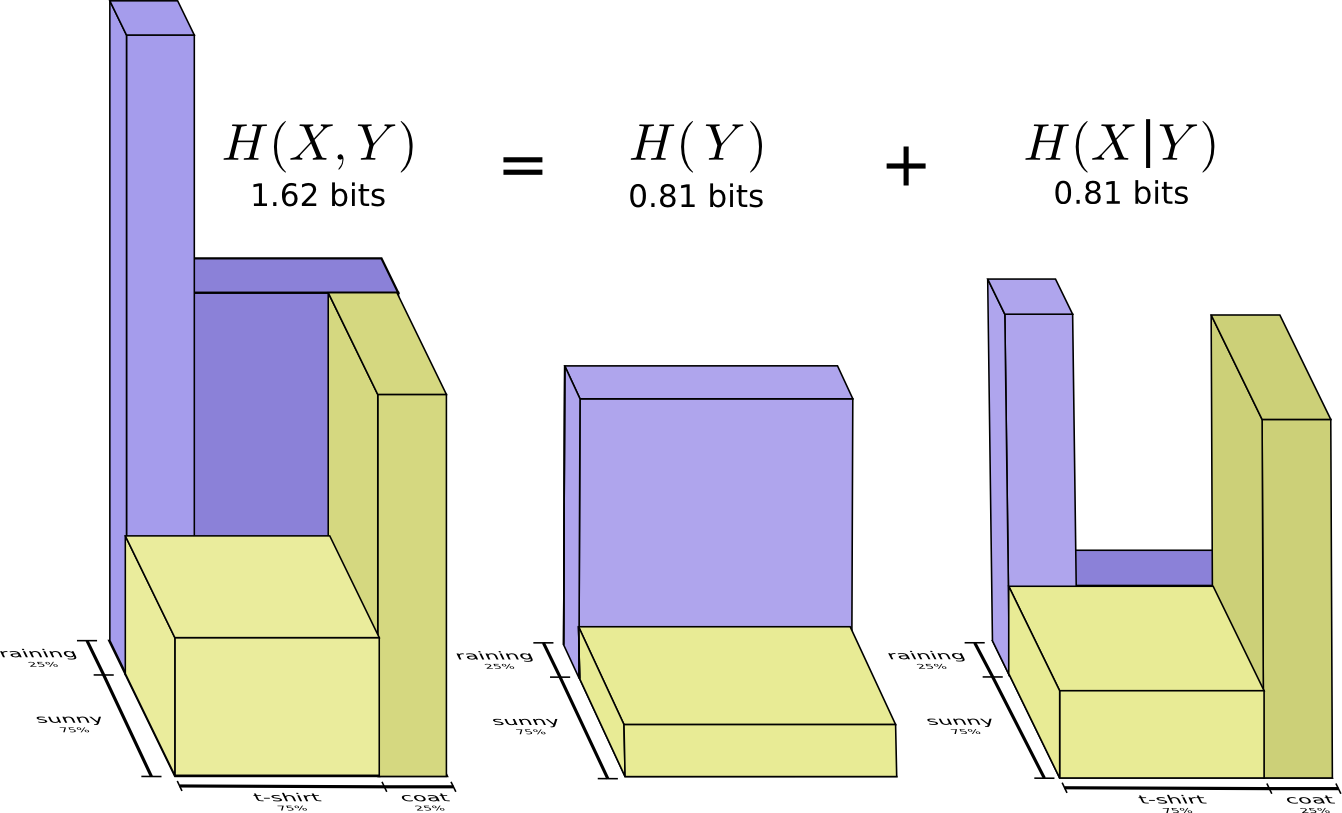
我们称其为联合熵 $$$X$ 和 $$$Y$ 定义如下：

$$

$$H（X，Y）= \ sum_ {x，y} p（x，y）\ log_2 \ bigg（\ frac {1} {p（x，y）} \ bigg）$$

它与我们通常的定义相吻合，只是两个变量而不是一个变量。

通过在第三维中表示代码字的长度，可以获得一个稍微好一点的图像，但没有使分布均匀。 现在熵就是体积！



但是，假设我母亲已经知道天气了。 她可以在新闻中看到她。 我需要提供多少信息？

看来我需要发送足够的信息来告诉我我穿什么衣服。 但是实际上，我需要发送的信息较少，因为我将要经历的天气很大程度上取决于天气！ 让我们分别看一下下雨和晒太阳的情况。



在这两种情况下，我平均不需要发送太多信息，因为天气让我很好地猜测正确答案是什么。 在太阳下时，我可以使用针对太阳优化的特殊代码，在下雨时，我可以使用针对雨优化的代码。 在两种情况下，发送的信息都少于两种情况下都使用通用代码的信息。 为了获得我需要发送给母亲的平均信息量，我将这两种情况放在一起...



我们称此为条件熵。 如果将其形式化为方程式，则会得到：

$$

$$H（X | Y）= \ sum_yp（y）\ sum_xp（x | y）\ log_2 \ bigg（\ frac {1} {p（x | y）} \ bigg）$$

$$

$$= \ sum_ {x，y} p（x，y）\ log_2 \ bigg（\ frac {1} {p（x | y）} \ bigg）$$

相互信息

在上一节中，我们发现了解一个变量可能意味着需要较少的信息来传达另一个变量的值。

考虑它的一个好方法是想象条带形式的信息量。 如果它们之间有共同的信息，则这些频段会重叠。 例如，其中的某些信息 $$$X$ 和 $$$Y$ 因此常见 $$$H（X）$ 和 $$$H（Y）$ 重叠的条纹。 由于 $$$H（X，Y）$ 是两个变量的信息，那么这就是波段的并集 $$$H（X）$ 和 $$$H（Y）$ 。



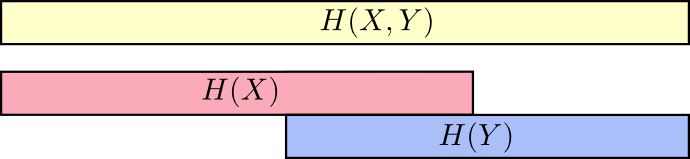
当我们以这种方式思考事物时，很容易看到很多东西。

例如，我们已经注意到， $$$X$ 所以和 $$$Y$ （“联合熵”， $$$H（X，Y）$ ）需要的信息比仅用于传输的信息更多 $$$X$ （“最终熵”， $$$H（X）$ ） 但是如果你已经知道 $$$Y$ 然后传输 $$$X$ （“条件熵”， $$$H（X | Y）$ ）所需的信息比您不知道的信息少！



听起来很复杂，但是如果您翻译成乐队，那么一切都会变得非常简单。 $$$H（X | Y）$ 是我们必须发送以告知的信息 $$$X$ 一个已经知道的人 $$$Y$ 信息在 $$$X$ 这也不在 $$$Y$ 。 在视觉上，这意味着 $$$H（X | Y）$ -这是地带的一部分 $$$H（X）$ 与...不重叠 $$$H（Y）$ 。

现在您可以阅读不平等 $$$H（X，Y）≥H（X）≥H（X | Y）$ 就在下一张图表上



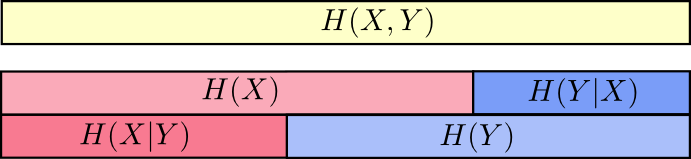
另一个相等如下： $$$H（X，Y）= H（Y）+ H（X | Y）$ 。 即 信息在 $$$X$ 和 $$$Y$ 这是信息 $$$Y$ 加上信息 $$$X$ 不在 $$$Y$ 。



同样，在等式中很难看到这一点，但是如果您考虑重叠的信息带则很容易看到。

至此，我们将信息分解为 $$$X$ 和 $$$Y$ 以几种方式。 我们知道每个变量中的信息， $$$H（X）$ 和 $$$H（Y）$ 。 我们知道这两种信息的结合 $$$H（X，Y）$ 。 我们的信息包含在一个变量中，而没有另一个变量， $$$H（X | Y）$ 和 $$$H（Y | X）$ 。 其中大部分围绕变量共同的信息-信息的交集。 我们称其为“相互信息” $$$（x，y）$ 定义为：

$$

$$I（X，Y）= H（X）+ H（Y）−H（X，Y）$$

这个定义是正确的，因为 $$$H（X）+ H（Y）$ 包含共同信息的两个副本，因为它也位于 $$$X$ 和在 $$$Y$ 一会儿 $$$H（X，Y）$ 只包含一个副本。 （请参见上图）

信息的变化与相互信息紧密相关。 信息变化是变量不共有的信息。 我们可以这样定义它：

$$

$$V（X，Y）= H（X，Y）−I（X，Y）$$

信息的变化很有趣，因为它为我们提供了一个度量标准，即不同变量之间的距离的概念。 如果知道一个变量的值告诉您另一个变量的含义，则两个变量之间的信息变化为零，并且随着它们变得更加独立而变大。

这与KL散度有何关系，这也给我们带来了距离的概念？ KL散度是同一变量或一组变量的两个分布之间的距离。 相反，信息的变化为我们提供了两个共同分布变量之间的距离。 KL散度是分布之间的差异，即分布内信息的变化。

我们可以将所有这些放到一个图表中，以链接所有这些不同类型的信息：

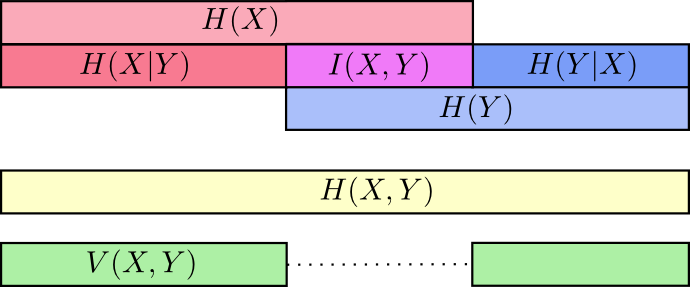
分数位

信息论中一个非常不直观的事情是我们可以拥有分数的位数。 这很奇怪。 一半是什么意思？

这是一个简单的答案：通常我们对消息的平均长度感兴趣，而不是对特定消息的长度感兴趣。 如果在一半情况下发送一个比特，而在一半情况下发送两个比特，则平均发送一个半比特。 平均值可以是分数的事实并不奇怪。

但是有了这个答案，我们回避了这个问题。 最佳码字长度通常也是分数。 这是什么意思？

具体来说，让我们看一下概率分布，其中一个事件 $$$一$ 发生了71％的时间，还有另一个事件， $$$b$ 发生29％的时间。



最佳代码将使用0.5位表示 $$$一$ 和1.7位代表 $$$b$ 。 好吧，如果我们只想发送这些代码字之一，那么这种表示是不可能的。 我们被迫舍入到整数位数，并平均发送1位。

...但是，如果我们同时发送多个消息，那么事实证明我们可以做得更好。 让我们考虑这个分布的两个事件的传递。 如果我们独立发送它们，则必须发送两个位。 我们如何改善呢？



在一半情况下，我们需要发送 $$$aa$ ，在21％的情况下- $$$ab$ 或 $$$ba$ ，而在8％的情况下- $$$bb$ 。 同样，理想代码包括小数位。



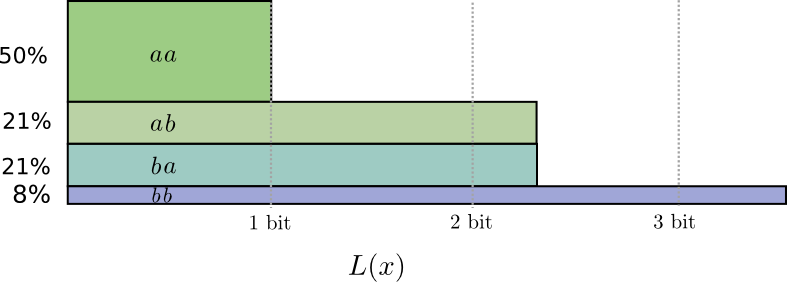
如果我们舍入代码字的长度，我们将得到如下内容：



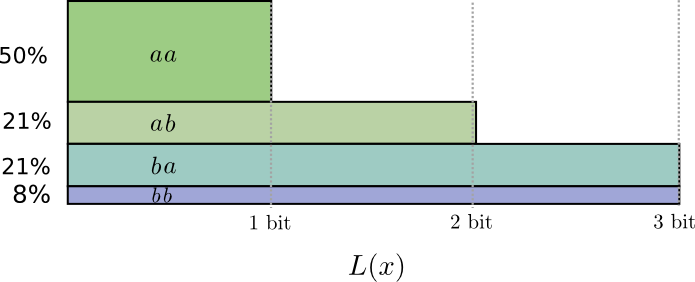
这些代码使我们的平均消息长度为1.8位。 当我们独立发送消息时，这少于2位。 即 在这种情况下，每个事件我们平均发送0.9位。 如果我们一次发送更多事件，则平均值将更低。 在 $$$n$ 趋于无穷大，与舍入我们的代码相关的开销将消失，并且每个代码字的位数将收敛到熵。

接下来，请注意事件的理想码字长度 $$$一$ 是0.5位，并且码字的理想长度 $$$aa$ -1位 理想的码字长度加起来，即使它们是分数！ 因此，如果我们一次报告多个事件，则长度将相加。

我们可以看到，即使实际代码只能使用整数，信息位数的小数位数还是有实际意义的。

（实际上，人们使用某些在不同情况下有效的编码方案。霍夫曼代码实际上是我们在此处绘制的那种代码，它不能非常优雅地处理小数位-您必须像上面那样对字符进行分组或使用更复杂的技巧以接近熵的极限。算术编码略有不同，它优雅地处理小数位以使其渐近最优。）

结论

如果我们关注最小位数的信息传输，那么这些想法当然是基本的。 如果我们关心数据压缩，则信息论解决了主要问题，并从根本上给了我们正确的抽象。 但是，如果我们不在乎，那会不会是异国情调？

信息理论的思想出现在许多情况下：机器学习，量子物理学，遗传学，热力学，甚至是赌博。 这些领域的从业者并不关心信息理论，因为他们想压缩信息。 他们关心它与他们的区域有着不可抗拒的联系。 量子纠缠可以用熵来描述。 通过假设关于您不知道的事物的最大熵，可以获得统计力学和热力学的许多结果。 玩家的得失与KL的发散直接相关，尤其是迭代设置。

信息论之所以出现在所有这些地方，是因为它为我们必须表达的许多事物提供了具体的，基本的形式化形式。 它为我们提供了测量和表达不确定性的方法，两组信念有何不同，一个问题的答案告诉我们另一组问题：概率有多分散，概率分布之间的距离以及这两个变量有多相关。 还有其他类似的想法吗？ 当然可以 但是，信息理论中的思想是纯粹的，它们确实具有很好的特性并且基于原理。 在某些情况下，这些想法正是您所需要的，而在其他情况下，它们是混乱世界中的便捷调停者。

机器学习是我最了解的知识，所以让我们一分钟谈一谈。 机器学习中一种非常常见的任务类型是分类。 假设我们要看一幅图片并预测它是狗还是猫的图片。 我们的模型可能会这样说：“这有80％的概率是狗的照片，有20％的概率是猫的照片。”假设正确的答案是狗-我们所说的概率是好是坏。 80％的狗是什么？85％的狗会更好吗？

这是一个重要的问题，因为我们需要对模型的优劣有一些了解，以便对其进行优化以取得成功。 我们应该优化什么？正确答案实际上取决于我们使用该模型的目的：我们是否仅在乎我们的猜测是否正确，还是在乎我们对正确答案的信心如何？自信地犯错有多糟糕？没有一个正确的答案。通常，不可能找到正确的答案，因为我们不知道该模型将如何用于形式化最终使我们兴奋的形式。在某些情况下，交叉熵确实使我们感到担忧，但这并非总是如此。通常，我们并不确切地知道什么让我们担心，交叉熵是一个很好的代理。

. ; , . – , , , , , — , .