 许多程序员认为快速排序是所有算法中最快的。 这部分是正确的。 但是,只有在正确选择了support元素的情况下,它才能很好地工作( 那么复杂度为O(n log n) )。 否则,渐近行为将与气泡的近似( 即O(n 2 ) )相同。
许多程序员认为快速排序是所有算法中最快的。 这部分是正确的。 但是,只有在正确选择了support元素的情况下,它才能很好地工作( 那么复杂度为O(n log n) )。 否则,渐近行为将与气泡的近似( 即O(n 2 ) )相同。
同时,如果已经对数组进行了排序,则该算法的运行速度不会比O(n log n)快
基于此,我决定编写自己的算法来对数组进行排序,该算法比quick_sort更好。 而且,如果数组已经排序,则不要像很多算法那样多次运行它。
“那是傍晚,没事可做,”-谢尔盖·米哈尔科夫(Sergei Mikhalkov)。
要求:
- 最佳情况O(n)
- O的平均情况(n log n)
- 最坏情况O(n log n)
- 平均比快速排序更快
现在让我们按顺序进行所有操作
为了使我们的算法始终快速运行,在一般情况下,渐近行为必须至少为O(n log n),最好为O(n)。 我们都知道,插入排序最多只能一次完成。 但是在最坏的情况下,她将不得不围绕阵列中的元素进行多次移动。
初步资料
合并两个数组的功能int* glue(int* a, int lenA, int* b, int lenB) { int lenC = lenA + lenB; int* c = new int[lenC];
合并两个数组的功能将结果保存到指定的数组中。 void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { if (lenA == 0) {
通过在lo和hi之间插入来进行排序的函数 void insertionSort(int*& arr, int lo, int hi) { for (int i = lo + 1; i <= hi; ++i) for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) swap(arr[j - 1], arr[j]); }
该算法的主要思想是所谓的搜索最大值(和最小值)。 在每次迭代时,从数组中选择一个元素。 如果它大于先前的最大值,则将此元素添加到选择的末尾。 否则,如果它小于先前的最小值,那么我们将此元素添加到开头。 否则,放置在单独的数组中。
输入函数接受一个数组以及此数组中的元素数
void FirstNewGeneratingSort(int*& arr, int len)
为了存储数组(我们的高点和低点)和其他元素中的样本,我们分配内存
int* selection = new int[len << 1];
如您所见,我们分配的样本存储空间是原始数组的2倍。 如果我们对数组进行了排序,并且每个下一个元素都是新的最大值,则可以这样做。 然后,仅样本数组的第二部分将被占用。 反之亦然(如果按降序排列)。
要进行采样,首先需要初始的最小值和最大值。 只需选择第一个和第二个元素
if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1];
抽样本身
for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i])
现在,我们有了一组排序的元素,还有我们仍然需要排序的“剩余”元素。 但是首先,您需要进行一些内存操作。
释放未使用的内存
int selectionLen = right - left - 1;
对其余元素进行递归排序调用,并将其与选择内容合并
FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen);
所有算法代码(非最佳版本) void FirstNewGeneratingSort(int*& arr, int len) { if (len < 2) return; int* selection = new int[len << 1]; int left = len - 1; int right = len; int* restElements = new int[len]; int restLen = 0; if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i])
与快速排序相比,让我们检查算法的速度
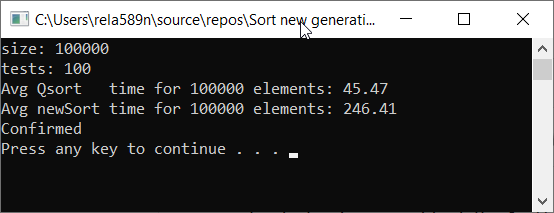
如您所见,这根本不是我们想要的。 比QuickSort快六倍! 但是在这种情况下,使用时间是不合适的,因为在这里重要的是渐近线。 在算法的这种实现中,在最坏的情况下,第一和第二元素将是最小和最大。 其余的将被复制到单独的数组中。
算法复杂度:
- 最坏的情况: O(n 2 )
- 中例: O(n 2 )
- 最佳情况: O(n)
嗯,这并不比通过插入进行相同的排序更好。 是的,的确,我们可以很快找到最大(最小)元素,而其他元素根本不会落入选择范围。
我们可以尝试优化合并排序。 首先,检查常规合并排序的速度:
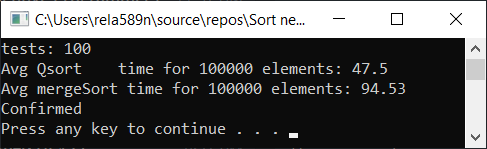
合并排序与优化: void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; if (hi - lo <= minPortion) {
为了便于使用,需要某种包装纸。
void newMergeSort(int *arr, int length) { int portion = log2(length);
测试结果:
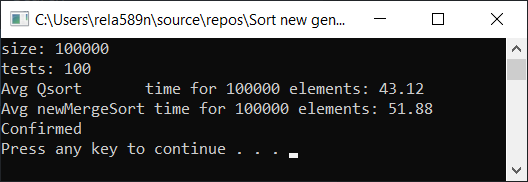
是的,可以观察到速度有所提高,但是,此功能不能像“快速排序”一样快。 而且,我们不能谈论排序数组上的O(n)。 因此,此选项也被丢弃。
第一个选项的优化选项
为了确保复杂度不为O(n 2 ),我们可以像以前一样在1个数组中添加未落入样本的元素,但将它们扩展为2个数组。 之后,仅需对这两个部分进行排序,然后将其与我们的示例合并。 结果,我们得到的复杂度等于O(n log n)
正如我们已经注意到的,可以很快找到排序数组中绝对最大(最小)的元素,但这不是很有效。 这是插入排序帮助我们的地方。 在每次选择的迭代中,我们将检查是否可以将flow元素插入到最后一个插入的集合中,例如,插入的八个元素。
如果现在不清楚,请不要难过。 应该是这样。 现在,代码中的所有内容将变得清晰,问题将消失。
签名与以前的版本相同
void newGenerationSort(int*& arr, int len)
但是应该注意,此选项假定一个指向第一个参数的指针,可以在该参数上调用delete []操作(为什么-我们将在后面看到)。 也就是说,当我们分配内存时,我们为此指针分配了数组开头的地址。
初步准备
在此示例中,所谓的“追赶系数”只是一个值为8的常数。它显示了我们尝试在其位置插入新的“低于最大值”或“低于最小值”的最大元素数。
int localCatchUp = min(catchUp, len);
要存储样本,请创建一个数组
如果不清楚,请参阅初始版本中的说明
int* selection = new int[len << 1];
填写选择数组的前几个元素
selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; }
让我提醒您,新的低点在样本数组中心的左侧,新的高点在右边
创建数组以存储未选择的项目
int restLen = len >> 1;
现在,最重要的是从源数组中正确选择元素
循环从localCatchUp开始(因为之前的元素已经作为示例开始输入我们的示例了)。 到最后。 因此,最后,所有元素都将分配到选择数组或欠选择数组之一中。
为了检查是否可以在选择中插入一个元素,我们只需检查它是否大于(或等于)左边8个元素的位置(右边-localCatchUp)。 如果是这种情况,那么我们只需将它们插入这些元素即可,将其插入所需的位置。 这是针对右侧,即针对最大元素。 以同样的方式,我们对最小的进行相反的处理。 如果您无法将其插入选择的任一侧,则将其放入其余数组之一。
循环看起来像这样:
for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] > selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) {
再说一遍,这是怎么回事? 首先,我们尝试将元素推高。 无法运作 -如果可能,将其扔到最低点。 如果也无法做到这一点-将其放在restFirst或restSecond中。
最困难的部分结束了。 现在,在循环之后,我们有了一个带选择的排序数组(元素从索引[left + 1]开始并在[right-1]结束 ),以及分别为restFirstLen和restSecondLen的 restFirst和restSecond数组 。
与上一个示例一样,在递归调用之前,我们从主数组中释放了内存(我们已经保存了所有元素)
delete[] arr;
我们的选择数组可以包含许多未使用的内存单元。 在递归调用之前,您需要释放它。
释放未使用的内存
int selectionLen = right - left - 1;
现在为restFirst和restSecond数组递归运行排序函数
要了解其工作原理,您首先需要看一下代码。 现在,您只需要相信在递归调用之后,将对restFirst和restSecond数组进行排序。
newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen);
最后,我们需要将3个数组合并为结果数组,并将其分配给指针arr。
您可以先将restFirst + restSecond合并到一些restFull数组中,然后再合并selection + restFull 。 但是此算法具有这样的属性,即与其他数组相比, 选择数组最有可能包含更少的元素。 假设选择包含100个元素, restFirst包含 990, restSecond包含 1010。然后,要创建restFull数组,您需要执行990 + 1010 = 2000复制操作。 然后与选择合并-另外2000 + 100份。 使用此方法的总计,总副本将为2000 + 2100 = 4100。
让我们在这里应用优化。 首先将选择和restFirst合并到选择数组中。 复制操作:100 + 990 =1090。接下来,合并选择数组和restSecond数组,再花费1090 + 1010 = 2100个副本。 总共将发布2100 + 1090 = 3190,这比以前的方法少了近四分之一。
数组的最终合并
int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen);
如您所见,如果我们将选择与restFirst合并起来更有利可图,那么我们这样做。 否则,我们将像“ restFull”中那样合并
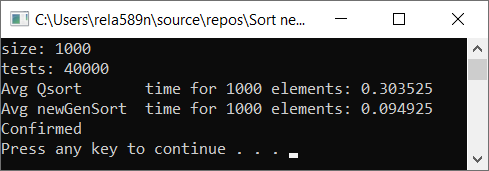
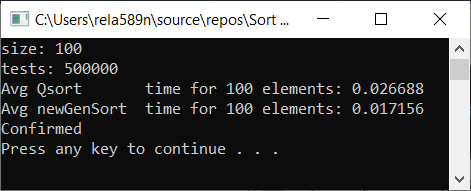
现在测试时间
Source.cpp中的主要代码: #include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h" using namespace std; using namespace rela589n; void printArr(int* arr, int len) { for (int i = 0; i < len; ++i) { cout << arr[i] << " "; } cout << endl; } bool arraysEqual(int* arr1, int* arr2, int len) { for (int i = 0; i < len; ++i) { if (arr1[i] != arr2[i]) { return false; } } return true; } int* createArray(int length) { int* a1 = new int[length]; for (int i = 0; i < length; i++) { a1[i] = rand(); //a1[i] = (i + 1) % (length / 4); } return a1; } int* array_copy(int* arr, int length) { int* a2 = new int[length]; for (int i = 0; i < length; i++) { a2[i] = arr[i]; } return a2; } void tester(int tests, int length) { double t1, t2; int** arrays1 = new int* [tests]; int** arrays2 = new int* [tests]; for (int t = 0; t < tests; ++t) { // int* arr1 = createArray(length); arrays1[t] = arr1; arrays2[t] = array_copy(arr1, length); } t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { quickSort(arrays1[t], 0, length - 1); } t2 = getCPUTime(); cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; int portion = catchUp = 8; t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { newGenerationSort(arrays2[t], length); } t2 = getCPUTime(); cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion << endl; bool confirmed = true; // for (int t = 0; t < tests; ++t) { if (!arraysEqual(arrays1[t], arrays2[t], length)) { confirmed = false; break; } } if (confirmed) { cout << "Confirmed" << endl; } else { cout << "Review your code! Something wrong..." << endl; } } int main() { srand(time(NULL)); int length; double t1, t2; cout << "size: "; cin >> length; int t; cout << "tests: "; cin >> t; tester(t, length); system("pause"); return 0; }
测试期间用于比较的Quick Sort实现:一句话:我使用了quickSort的这种特定实现,以便一切都是诚实的。 尽管算法库中的标准排序是通用的,但它的工作速度比下面介绍的慢2倍。
getCPUTime-CPU时间测量: #pragma once #if defined(_WIN32) #include <Windows.h> #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) #include <unistd.h> #include <sys/resource.h> #include <sys/times.h> #include <time.h> #else #error "Unable to define getCPUTime( ) for an unknown OS." #endif /** * Returns the amount of CPU time used by the current process, * in seconds, or -1.0 if an error occurred. */ double getCPUTime() { #if defined(_WIN32) /* Windows -------------------------------------------------- */ FILETIME createTime; FILETIME exitTime; FILETIME kernelTime; FILETIME userTime; if (GetProcessTimes(GetCurrentProcess(), &create;Time, &exit;Time, &kernel;Time, &user;Time) != -1) { SYSTEMTIME userSystemTime; if (FileTimeToSystemTime(&user;Time, &user;SystemTime) != -1) return (double)userSystemTime.wHour * 3600.0 + (double)userSystemTime.wMinute * 60.0 + (double)userSystemTime.wSecond + (double)userSystemTime.wMilliseconds / 1000.0; } #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) /* AIX, BSD, Cygwin, HP-UX, Linux, OSX, and Solaris --------- */ #if defined(_POSIX_TIMERS) && (_POSIX_TIMERS > 0) /* Prefer high-res POSIX timers, when available. */ { clockid_t id; struct timespec ts; #if _POSIX_CPUTIME > 0 /* Clock ids vary by OS. Query the id, if possible. */ if (clock_getcpuclockid(0, &id;) == -1) #endif #if defined(CLOCK_PROCESS_CPUTIME_ID) /* Use known clock id for AIX, Linux, or Solaris. */ id = CLOCK_PROCESS_CPUTIME_ID; #elif defined(CLOCK_VIRTUAL) /* Use known clock id for BSD or HP-UX. */ id = CLOCK_VIRTUAL; #else id = (clockid_t)-1; #endif if (id != (clockid_t)-1 && clock_gettime(id, &ts;) != -1) return (double)ts.tv_sec + (double)ts.tv_nsec / 1000000000.0; } #endif #if defined(RUSAGE_SELF) { struct rusage rusage; if (getrusage(RUSAGE_SELF, &rusage;) != -1) return (double)rusage.ru_utime.tv_sec + (double)rusage.ru_utime.tv_usec / 1000000.0; } #endif #if defined(_SC_CLK_TCK) { const double ticks = (double)sysconf(_SC_CLK_TCK); struct tms tms; if (times(&tms;) != (clock_t)-1) return (double)tms.tms_utime / ticks; } #endif #if defined(CLOCKS_PER_SEC) { clock_t cl = clock(); if (cl != (clock_t)-1) return (double)cl / (double)CLOCKS_PER_SEC; } #endif #endif return -1; /* Failed. */ }
所有测试均以百分之一的百分比在机器上执行。 英特尔酷睿i3 7100u和8GB RAM
部分有序数组 a1[i] = (i + 1) % (length / 4);


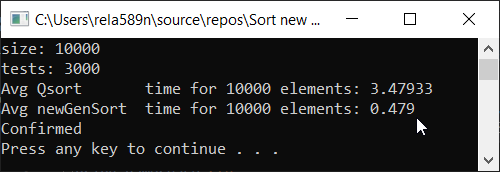
结论
如您所见,该算法行之有效。 至少我们想要的全部实现了。 以不确定性为代价,我不确定自己没有检查。 您可以自己检查。 但是从理论上讲,应该很容易实现。 在某些地方,放置≥或其他符号,而不是>符号。