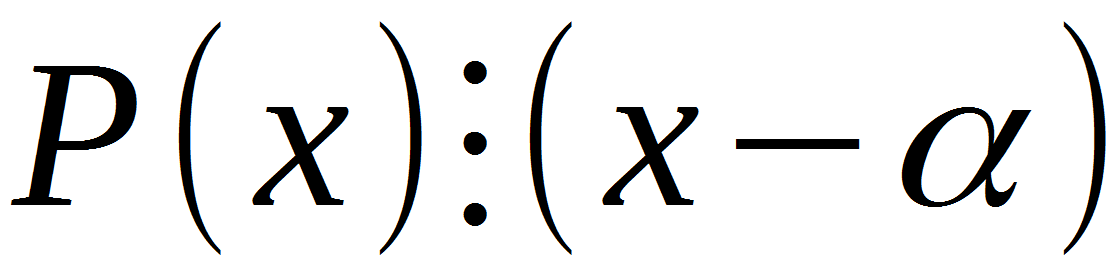
通常,在物理学,计算机科学和经济学中,我们面临最简单的线性或分数阶有理方程,而较少遇到二次方程。 那么第三和第四阶方程呢? 如果您有兴趣,那么我要一只猫。
首先,考虑最高阶方程的概念。 最高次方程为以下形式的方程:

在本文中,我将考虑:
1.三次方程。
2.可回收立方。
3. Horner方案和Bezout定理的应用。
4.可返回的二次方程。
三次方程
三次方程式是其中高级程度未知的未知度的方程式,三次方程式具有以下形式:

这样的方程可以用不同的方法求解,但是,我们将利用基础知识,并通过分组方法求解三次方程:

在此示例中,使用分组方法,我们将前两个成员和最后两个成员分组,得到相等的括号,再次得出,得到两个括号的方程式。
然后乘积等于零,并且只有在至少一个因子等于零的情况下,基于此,我们才将每个因子(方括号)都等于零,从而获得不完整的二次方程和线性方程。
还值得注意的是,方程的最大根数等于前导项未知的阶数,因此在三次方程式中最多可以有3个根,在双二次(第4级)中最多不能有4个根。 等
返回三次方程
返回三次方程的形式为:

它们被称为可返回的,因为这些系数将被镜像。 相似的方程式也可以通过学校的方法来求解,但是要棘手一些:

首先,进行分组,然后使用缩写乘法的公式,分解得到的因子。 同样,我们得到2个相等的括号,“我们将其取出”。 我们得到两个因子(括号),并将它们作为两个不同的方程式求解。
Bezout定理和Horner方案
令人惊奇的是,法国数学家埃蒂安·贝祖特(Etienne Bezout)发现了贝祖特的定理,他主要研究代数。 Bezout定理可以表示为:

让我们弄清楚。 P(x)是x中的任意多项式,(x-a)是二项式,其中a是我们在自由项的除数中找到的方程式的全部根之一。
三点,这是一个运算符,指示一个表达式被另一个表达式除。 由此可知,找到了给定方程的至少一个根后,我们可以将此定理应用于该定理。 但是为什么需要这个定理,它的作用是什么? 如果您想降低多项式的次数,则Bezout定理是一个通用工具。 例如,在其帮助下,三次方程可以变成正方形,双二次方程,三次方程等。
但这是一回事,但如何划分呢? 当然,您可以将其划分为一列,但是这种方法并非所有人都可以使用,并且犯错的可能性非常高。 因此,还有另一种方式,这就是霍纳的方案。 我将举例说明她的工作。 假设:

因此,我们得到了一个多项式,并且可能已经提前找到了其中的一个根。 现在,我们绘制一个由6列和2行组成的小板,在第一行的每一列(第一行除外)中,我们引入方程的系数。 然后在第2行的第一列中添加a(找到的根)的值。 然后,在我们的案例5中,第一个系数就被吹灭了。 以下各列的值计算如下:

(图片是
在这里借来的)
接下来,我们对其余的列进行相同的操作。 最后一列(2行)的值将是除法的余数,在我们的示例中为0,如果您获得的数字不是0,则需要选择其他方法。 三次方程式的示例:

可返回的二次方程
我们还在上面考虑了回归三次方程,现在我们分析了二次方程。 他们的普遍看法:

与三次回归方程不同,并不是每个人的系数都是双二次的,但是在其他方面却非常相似。 这是求解此类方程式的算法:

如您所见,求解此类方程式并不简单。 但是我还是要弄清楚这种情况。 解开始于将整个方程除以x ^ 2。 接下来,我们进行分组,在这里我专门介绍了一条额外的代码以使内容更加清晰。 此后,我们将完成技巧,然后将第一个括弧2放入,我们首先将其相加然后相减,该金额无论如何都不会改变,但是现在我们可以将此括弧折叠成总和的平方。
我们从括号中删除-2,首先将其乘以a,然后引入新变量t并得到二次方程。
现在让我们继续一个例子:

如在通用算法中一样,主要部分被x ^ 2除,分组,折叠成一个完整的正方形,我们执行变量替换并求解二次方程。 之后,我们将获得的根代回,并求解2个二次方程(乘以x)。
应用领域
由于它们的庞大性和特殊性,高阶方程很少能找到它们的应用。 然而,仍然有一些例子,物理学中的绝热过程的泊松方程。
结论
在本文中,我仅考虑三次方程和双二次方程。 但是,考虑到的Bezout定理(和Horner方案)也可以用于求解5、6、7等度数的方程,即使它们的应用受到限制。