
在Serokell,我们不仅从事商业项目,而且致力于使世界变得更好。 例如,我们正在努力改善所有Haskelists的主要工具-格拉斯哥Haskell编译器(GHC)。 在Richard Eisenberg的著作“ Haskell中的从属类型:理论与实践”的影响下,我们专注于扩展类型系统。
弗拉迪斯拉夫(Vladislav)在我们的博客中已经讨论了Haskell为什么缺少依赖类型以及我们计划如何添加它们。 我们决定将这篇文章翻译成俄语,以便尽可能多的开发人员可以使用依赖类型,并为Haskell语言的发展做出进一步的贡献。
现状
我在Haskell中最想念依赖类型。 让我们讨论为什么。 从我们想要的代码中:
- 性能,即执行速度和低内存消耗;
- 可维护性和易于理解;
- 编译方法保证了正确性。
使用现有技术,几乎不可能实现所有这三个特征,但是通过支持Haskell依赖类型,任务得以简化。
Haskell标准:人机工程学+性能
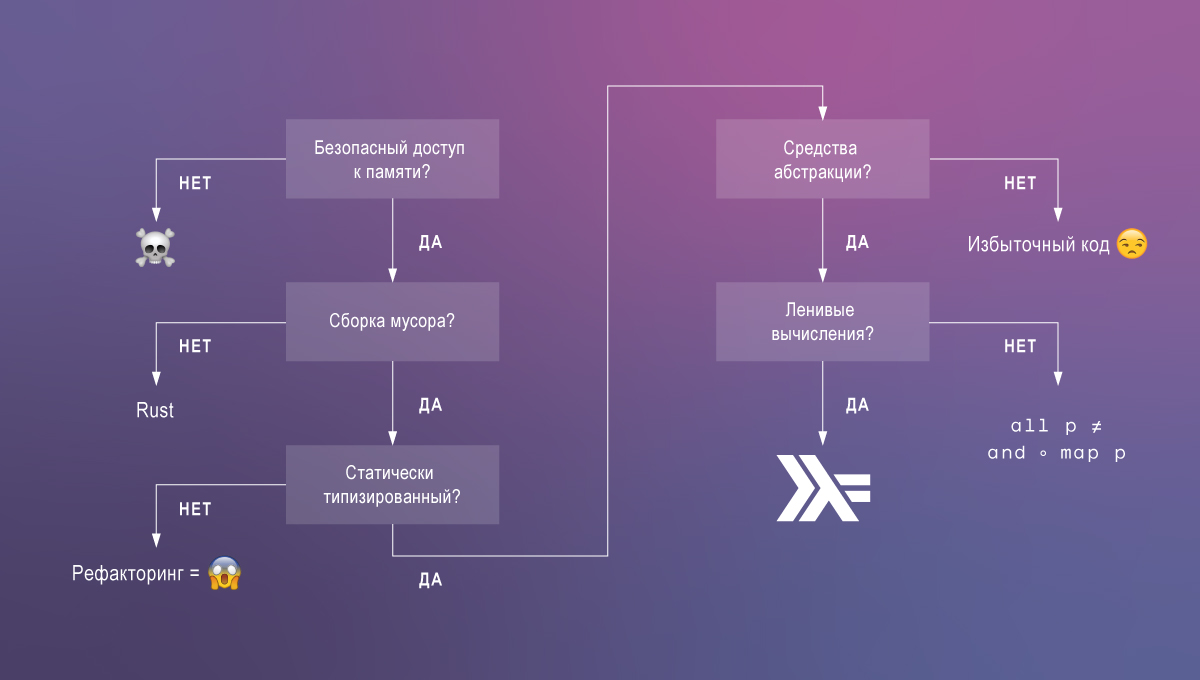
Haskell基于一个简单的系统:具有惰性计算,代数数据类型和类型类的多态Lambda演算。 正是这些语言功能的组合,使我们能够编写优美,受支持且高效的代码。 为了证实这一说法,我们将Haskell与更多流行语言进行了简要比较。
内存访问不安全的语言(例如C)会导致最严重的错误和漏洞(例如,缓冲区溢出,内存泄漏)。 有时需要这种语言,但大多数情况下它们的使用是马马虎虎的想法。
安全内存访问语言分为两类:依赖垃圾回收器的语言和Rust。 Rust在提供无垃圾收集的安全访问内存方面似乎是独一无二的。 该组中也不再支持Cyclone和其他研究语言。 但是与他们不同的是,Rust正在走向流行。 缺点是,尽管具有安全性,Rust的内存管理也不是简单且手动的。 在可以使用垃圾收集器的应用程序中,最好将开发人员的时间花在其他任务上。
剩下有垃圾收集器的语言,我们将根据它们的类型系统将其进一步分为两类。
动态类型(或更确切地说是单类型)语言(例如JavaScript或Clojure)不提供静态分析,因此无法对代码的正确性提供相同的置信度(并且不能,测试不能替换类型-两者都需要) !)。
诸如Java或Go之类的静态类型语言通常具有非常有限的类型系统。 这迫使程序员编写冗余代码,并放置不安全的语言功能。 例如,Go中缺乏通用类型会强制使用接口{}和强制转换运行时类型 。 具有副作用(输入,输出)的计算与纯计算之间也没有分隔。
最后,在具有安全内存访问,垃圾回收器和功能强大的类型系统的语言中,Haskell在惰性方面脱颖而出。 惰性计算对于编写可组合的模块化代码非常有用。 它们使将表达式的任何部分分解为辅助定义成为可能,包括定义控制流的构造。
Haskell似乎是一种几乎完美的语言,直到您认识到与静态证明相比与Agda等定理证明工具相比,Haskell与释放其全部潜力有多远。
作为Haskell类型系统功能不够强大的简单示例,请考虑Prelude的列表索引运算符(或从primitive包中索引数组 ):
(!!) :: [a] -> Int -> a indexArray :: Array a -> Int -> a
这些类型签名中的任何内容都不能反映索引必须为非负且小于集合长度的要求。 对于具有高可靠性要求的软件,这是不可接受的。
Agda:人体工程学+正确性
定理的证明手段(例如Coq )是允许使用计算机开发数学定理的形式证明的软件工具。 对于数学家而言,使用此类工具就像在纸上书写证据。 计算机确定这种证据的有效性所要求的空前严格程度之间的差异。
但是,对于程序员而言,证明定理的方法与具有难以置信的类型系统(甚至可能是集成开发环境)的深奥编程语言的编译器并没有什么不同,而其他方面的性能却中等(甚至不存在)。 证明定理的一种方法实际上是编程语言,编程语言的作者花了所有时间开发打字系统,却忘记了仍然需要运行程序。
经过验证的软件开发人员的梦想是证明定理的一种方法,这将是具有高质量代码生成器和运行时的良好编程语言。 在这个方向上,包括伊德里斯的创造者进行了实验。 但这是一种具有严格的(精力充沛的)计算语言,并且目前其实现还不稳定。
在证明定理的所有方法中,阿格达·哈斯克尔主义者最喜欢。 在许多方面,它与Haskell类似,但具有更强大的类型系统。 我们在Serokell使用它来证明我们程序的各种特性。 我的同事Dania Rogozin写了一系列有关此的文章 。
这是类似于Haskell运算符(!!)的查找函数类型:
lookup : ∀ (xs : List A) → Fin (length xs) → A
这里的第一个参数的类型为List A ,它对应于Haskell中的[a] 。 但是,我们将其命名为xs ,以在其余类型签名中引用它。 在Haskell中,我们只能在术语级别的函数主体中访问函数参数:
(!!) :: [a] -> Int -> a
但是在Agda中,我们可以在类型级别引用此xs值,这在第二个lookup参数Fin (length xs) 。 在类型级别引用其参数的函数称为相关函数,并且是相关类型的示例。
lookup的第二个参数的类型为Fin n , n ~ length xs 。 Fin n类型的值对应于[0, n)范围内的数字,因此Fin (length xs)是一个小于输入列表长度的非负数。 这正是我们需要提供列表项的有效索引的条件。 粗略地说, lookup ["x","y","z"] 2将通过类型检查,但是lookup ["x","y","z"] 42将失败。
关于运行Agda程序,我们可以使用MAlonzo 后端在Haskell中对其进行编译。 但是生成的代码的性能将不能令人满意。 这不是MAlonzo的错:他必须插入许多unsafeCoerce以便GHC unsafeCoerce Agda已验证的代码。 但是,相同的unsafeCoerce 会降低性能 (在本文讨论之后,事实证明性能问题可能是由其他原因引起的-作者的注释) 。
这使我们陷入困境:我们必须使用Agda进行建模和形式验证,然后在Haskell上重新实现相同的功能。 通过这种工作流程的组织,我们的Agda代码可作为计算机验证的规范。 这比自然语言规范要好,但远非理想。 目的是如果代码被编译,那么它将按照规范工作。
具有扩展功能的Haskell:正确性和性能

为了对具有依赖类型的语言进行静态保证,GHC已经走了很长一段路。 扩展已添加到其中,以增加类型系统的表现力。 当GHC 7.4是编译器的最新版本时,我开始使用Haskell。 即使这样,它仍然具有高级类型级别编程的主要扩展: RankNTypes , GADTs , TypeFamilies , DataKinds和PolyKinds 。
尽管如此,Haskell中仍然没有成熟的依赖类型:既没有依赖函数(Π型)也没有依赖对(Σ型)。 另一方面,至少我们有一个编码!
当前的做法如下:
- 将类型级别的功能编码为私有类型族,
- 使用功能化来启用不饱和功能,
- 使用单个类型弥合术语和类型之间的鸿沟。
这导致了大量的冗余代码,但是singletons库通过Template Haskell自动生成了代码。
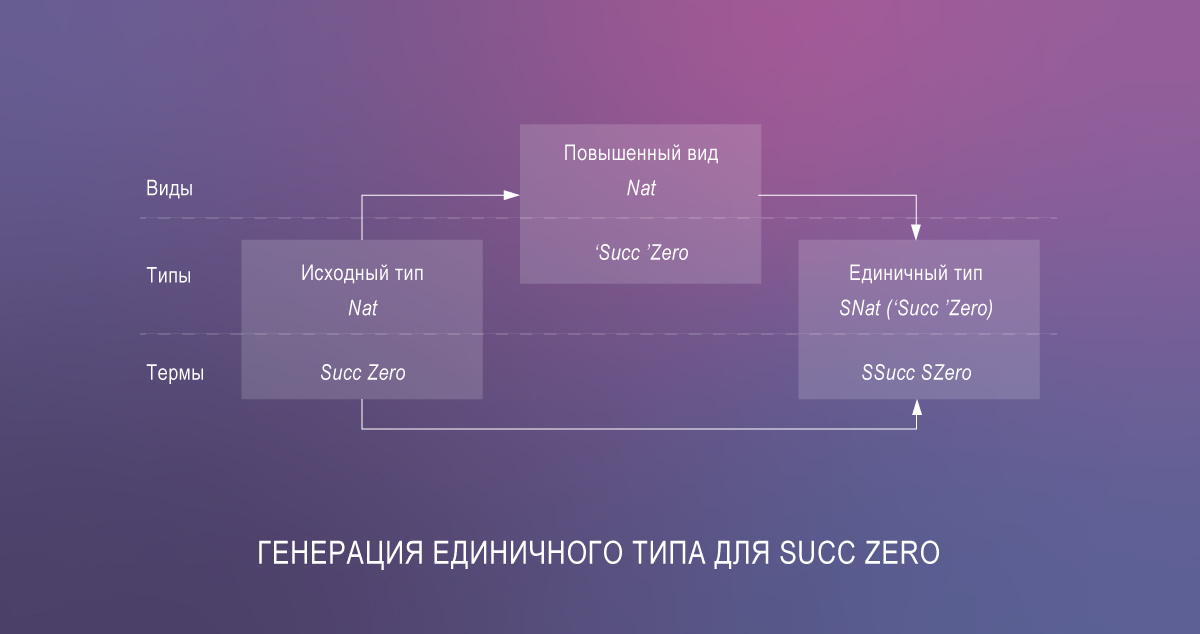
因此,最勇敢和果断的任务可以立即在Haskell中对依赖类型进行编码。 作为演示,这是类似于Agda上的变体的lookup功能的实现:
{-# OPTIONS -Wall -Wno-unticked-promoted-constructors -Wno-missing-signatures #-} {-# LANGUAGE LambdaCase, DataKinds, PolyKinds, TypeFamilies, GADTs, ScopedTypeVariables, EmptyCase, UndecidableInstances, TypeSynonymInstances, FlexibleInstances, TypeApplications, TemplateHaskell #-} module ListLookup where import Data.Singletons.TH import Data.Singletons.Prelude singletons [d| data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) |] data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: SingKind a => SList (xs :: [a]) -> Fin (Len xs) -> Demote a lookupS SNil = \case{} lookupS (SCons x xs) = \case FZ -> fromSing x FS i' -> lookupS xs i'
这是一个GHCi会话,它显示lookupS确实拒绝太大的索引:
GHCi, version 8.6.2: http://www.haskell.org/ghc/ :? for help [1 of 1] Compiling ListLookup ( ListLookup.hs, interpreted ) Ok, one module loaded. *ListLookup> :set -XTypeApplications -XDataKinds *ListLookup> lookupS (sing @["x", "y", "z"]) FZ "x" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS FZ) "y" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS FZ)) "z" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) <interactive>:5:34: error: • Couldn't match type ''S n0' with ''Z' Expected type: Fin (Len '["x", "y", "z"]) Actual type: Fin ('S ('S ('S ('S n0)))) • In the second argument of 'lookupS', namely '(FS (FS (FS FZ)))' In the expression: lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) In an equation for 'it': it = lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ)))
这个例子表明可行性并不意味着实用。 我很高兴Haskell具有实现lookupS语言功能,但与此同时,我也担心会出现不必要的复杂性。 在研究项目之外,我不建议使用这种代码样式。
在这种特殊情况下,我们可以使用长度索引向量以更少的复杂度获得相同的结果。 但是,Agda的直接代码翻译可以更好地揭示您在其他情况下必须遇到的问题。
以下是其中一些:
- 输入关系
a :: t和形式为t :: k的目标关系不同。 5 :: Integer在术语上是正确的,但在类型上不是。 "hi" :: Symbol在类型上正确,但在术语上不正确。 这使得Demote类型Demote必须映射视图和类型。 - 标准库使用
Int表示列表索引( singletons在提升的定义中使用Nat )。 Int和Nat是非归纳类型。 尽管比自然数的一元编码更有效,但它们在归纳定义(例如Fin或lookupS不能很好地工作。 因此,我们将length重新定义为len 。 - Haskell没有将功能提升到类型级别的内置机制。
singletons将其编码为私有类型族,并应用功能化来避免缺乏部分使用类型族。 这种编码很复杂。 另外,我们必须将len定义放在Template Haskell引号中,以便singletons生成其类型级别的对应项Len 。 - 没有内置的依赖功能。 人们必须使用单位类型来弥合术语和类型之间的鸿沟。 我们将
SList传递给lookupS输入,而不是通常的列表。 因此,我们必须牢记列表的几个定义。 这也导致程序执行期间的开销。 它们的出现是由于普通值和单位类型的值之间的转换( toSing , fromSing )以及转换过程的转移( SingKind限制)。
不便是较小的问题。 更糟糕的是,这些语言功能不可靠。 例如,我在2016年报告了问题#12564 ,同年还有#12088 。 与教科书中的示例(例如索引列表)相比,这两个问题都阻碍了更高级程序的实现。 这些GHC错误仍未修复,在我看来,原因是开发人员根本没有足够的时间。 积极从事GHC工作的人数非常少,因此有些事情无法解决。
总结
前面我提到过,我们需要代码中的所有三个属性,因此下面的表格说明了当前的事务状态:
美好的未来
在三个可用选项中,每个都有其缺点。 但是,我们可以修复它们:
- 使用标准的Haskell并直接添加从属类型,而不是通过
singletons进行不便编码。 (说起来容易做起来难。) - 以Agda为例,为其实现高效的代码生成器和RTS。 (说起来容易做起来难。)
- 将Haskell与扩展一起使用,修复错误并继续添加新扩展以简化相关类型的编码。 (说起来容易做起来难。)
好消息是,这三个选项都在某一点上收敛。 想象一下标准Haskell的最小扩展,该扩展添加了依赖类型,因此可以让您通过编写代码的方式保证代码的正确性。 可将Agda代码编译(转换)成这种语言,而无需使用unsafeCoerce 。 从某种意义上说,具有扩展功能的Haskell是该语言的未完成原型。 有些事情需要改进,而某些事情需要消除,但是最后,我们将达到预期的结果。
摆脱singletons
进步的一个很好的指标是singletons库的简化。 由于在Haskell中实现了依赖类型,因此不再需要变通方法和对singletons例实现的特殊情况的特殊处理。 最终,对该软件包的需求将完全消失。 例如,在2016年,使用-XTypeInType扩展名-XTypeInType我从SingKind和SomeSing 删除了 SomeSing 。 通过类型和类型的并集可以实现此更改。 比较新旧定义:
class (kparam ~ 'KProxy) => SingKind (kparam :: KProxy k) where type DemoteRep kparam :: * fromSing :: SingKind (a :: k) -> DemoteRep kparam toSing :: DemoteRep kparam -> SomeSing kparam type Demote (a :: k) = DemoteRep ('KProxy :: KProxy k) data SomeSing (kproxy :: KProxy k) where SomeSing :: Sing (a :: k) -> SomeSing ('KProxy :: KProxy k)
在旧的定义中, k出现在视图位置中,形式为t :: k的注释的右侧。 我们使用kparam :: KProxy k将k为类型。
class SingKind k where type DemoteRep k :: * fromSing :: SingKind (a :: k) -> DemoteRep k toSing :: DemoteRep k -> SomeSing k type Demote (a :: k) = DemoteRep k data SomeSing k where SomeSing :: Sing (a :: k) -> SomeSing k
在新的定义中, k在视图位置和类型位置之间自由移动,因此我们不再需要KProxy 。 原因是,从GHC 8.0开始,类型和类型属于同一句法类别。
在标准的Haskell中,存在三个完全独立的世界:术语,类型和视图。 如果您查看GHC 7.10的源代码,则可以看到单独的视图解析器和单独的check 。 GHC 8.0不再具有它们:类型和视图的解析器和验证很常见。
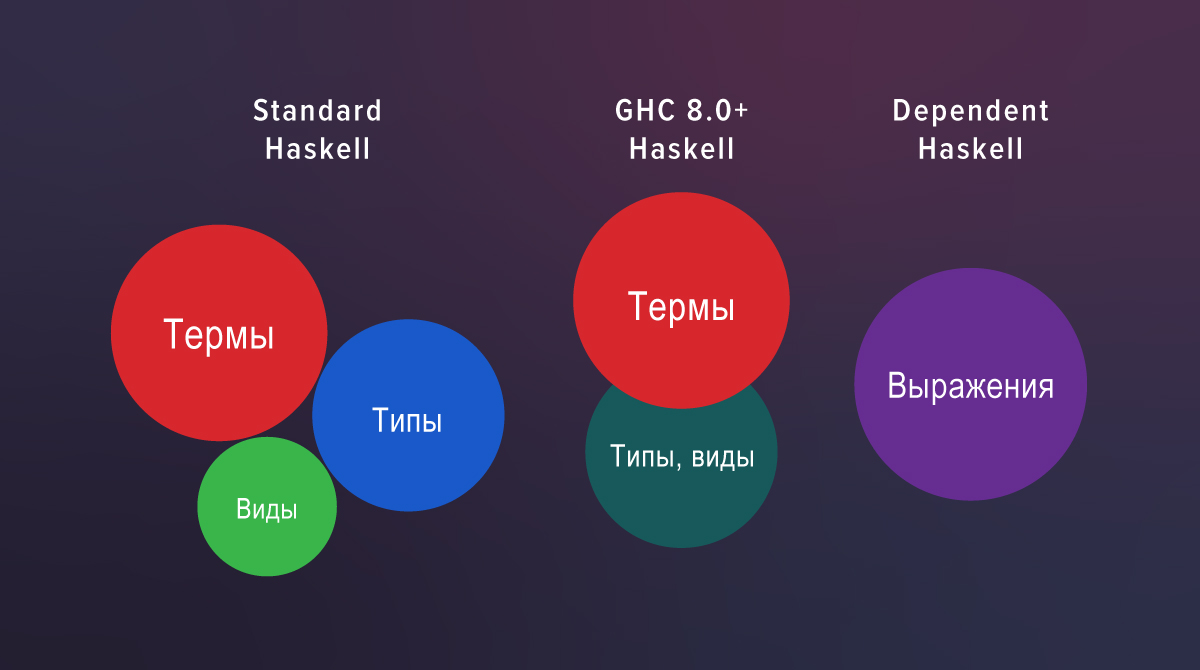
在具有扩展功能的Haskell中,视图只是类型所扮演的角色:
f :: T z -> ...
在GHC 8.0–8.4中,类型和类型之间的名称解析之间仍然存在一些差异。 但是我将它们最小StarIsType GHC 8.6:我创建了StarIsType扩展,并在PolyKinds引入了TypeInType功能。 我将其余的差异作为对GHC 8.8的警告 ,并在GHC 8.10中完全消除了它们 ( 本段的翻译已更新,原来的工作被描述为将来的任务-作者的注释 )。
下一步是什么? 让我们看看最新版本的singletons中的SingKind :
class SingKind k where type Demote k = (r :: Type) | r -> k fromSing :: Sing (a :: k) -> Demote k toSing :: Demote k -> SomeSing k
必须使用Demote类型Demote来解决打字关系a :: t和形式t :: k的目标关系之间的差异。 大多数情况下(对于代数数据类型), Demote是一种身份映射:
type Demote Bool = Booltype Demote [a] = [Demote a]type Demote (Either ab) = Either (Demote a) (Demote b)
因此, Demote (Either [Bool] Bool) = Either [Bool] Bool 。 此观察提示我们进行以下简化:
class SingKind k where fromSing :: Sing (a :: k) -> k toSing :: k -> SomeSing k
不需要Demote ! 而且,实际上,这将同时适用于Either [Bool] Bool和其他代数数据类型。 但是,实际上,我们正在处理非代数数据类型: Integer, Natural , Char , Text等。 如果用作物种,则不会填充它们: 1 :: Natural在术语级别为true,但在类型级别不是。 因此,我们正在处理以下定义:
type Demote Nat = Natural type Demote Symbol = Text
解决此问题的方法是提高基本类型。 例如, Text定义如下:
如果我们将ByteArray#和Int#适当地提高到类型级别,则可以使用Text而不是Symbol 。 通过对Natural和可能的其他几种类型进行相同的处理,可以摆脱Demote吧?
las,不是这样。 在上面,我对最重要的数据类型:函数视而不见。 它们还有一个特殊的Demote实例:
type Demote (k1 ~> k2) = Demote k1 -> Demote k2 type a ~> b = TyFun ab -> Type data TyFun :: Type -> Type -> Type
~>这是基于私有类型族和功能化以单例形式编码类型级别函数的类型。
起初,将~>和->组合起来似乎是一个好主意,因为两者均表示函数的类型(类型)。 问题是在类型位置的->和在视图位置的->表示不同的意思。 在术语级别,从a到b所有函数的类型a -> b 。 在类型级别上,只有从a到b 构造函数的类型a -> b ,但它们不是类型的同义词,也不是类型族。 为了推断类型,GHC假定f〜g和a〜b跟随fa ~ gb ,这对于构造函数而言是正确的,但对函数而言并非如此-这就是为什么有限制的原因。
因此,为了将函数提升到类型级别,但保留类型推断,我们将必须将构造函数移至单独的类型。 我们称其为a :-> b ,因为fa ~ gb从fa ~ gb跟随是真的。 其他功能仍将是a- a -> b类型。 例如, Just :: a :-> Maybe a ,但同时是isJust :: Maybe a -> Bool 。
Demote完成后,最后一步是摆脱Sing本身。 为此,我们需要一个新的量词,即forall和->的混合体。 让我们仔细看看isJust函数:
isJust :: forall a. Maybe a -> Bool isJust = \x -> case x of Nothing -> False Just _ -> True
使用类型a参数化isJust函数,然后使用值x :: Maybe a 。 这两个参数具有不同的属性:
- 明确的。 在
isJust (Just "hello")调用中,我们显式传递x = Just "hello" ,并且编译器隐式输出a = String 。 在现代的Haskell中,我们还可以强制两个参数的显式传递: isJust @String (Just "hello") 。 - 相关性 传递给代码中
isJust的输入的值也将在程序执行过程中传输:我们进行case匹配以验证其为Nothing或Just 。 因此,该值被认为是相关的。 但是它的类型已删除,无法与模式进行比较:该函数处理Maybe Int , Maybe String , Maybe Bool等。 因此,这被认为是无关紧要的。 此属性也称为参数性。 - 成瘾。 总而言之
forall a. t ,类型t可能引用a ,因此取决于传递的a 。 例如, isJust @String的类型Maybe String -> Bool是Maybe String -> Bool isJust @String Maybe String -> Bool ,而isJust @Int的类型Maybe Int -> Bool是Maybe Int -> Bool isJust @Int Maybe Int -> Bool 。 这意味着, forall是一个依赖量词。 请注意与value参数的区别:不管我们叫isJust Nothing还是isJust (Just …) ,结果类型始终为Bool 。 因此, ->是一个独立的量词。
要提取Sing ,我们需要一个明确且相关的量词,例如forall (a :: k). t a -> b ,同时还需要一个量词,例如forall (a :: k). t 。 将其表示为foreach (a :: k) -> t 。 为了取出SingI ,我们还引入了一个隐式相关依赖量词foreach (a :: k). t 。 结果,由于我们只向语言添加了相关函数,因此不再需要singletons 。
简要了解具有相关类型的Haskell
随着函数上升到类型级别和foreach量词的水平,我们可以如下重写lookupS :
data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: foreach (xs :: [a]) -> Fin (len xs) -> a lookupS [] = \case{} lookupS (x:xs) = \case FZ -> x FS i' -> lookupS xs i'
简而言之,代码没有,但是singletons代码很好地隐藏了冗余代码。 但是,新代码要简单得多:不再有SingKind , SList , SNil , SNil , SCons和fromSing 。 没有使用TemplateHaskell ,因为现在我们可以直接调用len函数,而不用创建Len类型族。 性能也将更好,因为您不再需要转换fromSing 。
我们仍然必须将length重新定义为len以返回归纳定义的N而不是Int 。 也许不应该将此问题视为将依赖类型添加到Haskell的一部分,因为Agda在lookup函数中还使用了归纳定义的N
在某些方面,具有依赖类型的Haskell甚至比标准Haskell更简单。 就此而言,类型和类型仍然组合为一种统一的语言。 我可以轻松想象在商业项目中以这种方式编写代码以正式证明关键应用程序组件的正确性。 许多Haskell库可以提供更安全的接口,而不会导致singletons的复杂性。
这将不容易实现。 我们面临着许多工程问题,这些问题影响到GHC的所有组件:解析器,名称解析,类型检查,甚至是核心语言。 一切都需要修改,甚至完全重新设计。
词库